
| 4 |
| 5 |
| 5 |
| 13 |
| π |
| 2 |
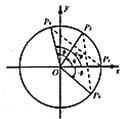 解:(1)①如图,在直角坐标系xOy内做单位圆O,
解:(1)①如图,在直角坐标系xOy内做单位圆O,| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 5 |
| 13 |
| π |
| 2 |
| 12 |
| 13 |
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 56 |
| 65 |


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
 某人计划开垦一块面积为32平方米的长方形菜地,同时要求菜地周围要留出前后宽2米,左右宽1米的过道(如图),设菜地的长为x米.
某人计划开垦一块面积为32平方米的长方形菜地,同时要求菜地周围要留出前后宽2米,左右宽1米的过道(如图),设菜地的长为x米.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
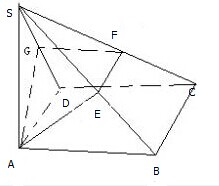 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.
已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 7 |
| 12 |
| 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com