
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题中“类”的理解,在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,对于各个结论进行分析:①∵2014÷5=402…4;②∵-3÷5=0…2,③整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4];④从正反两个方面考虑即可.
解答 解:①∵2014÷5=402…4,∴2014∈[4],故①对;
②∵-3=5×(-1)+2,∴对-3∉[3];故②错;
③∵整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4],故③对;
④∵整数a,b属于同一“类”,∴整数a,b被5除的余数相同,从而a-b被5除的余数为0,反之也成立,故“整数a,b属于同一“类”的充要条件是“a-b∈[0]”.故④对.
∴正确结论的个数是3.
故选:C.
点评 本题主要考查了选修3同余的性质,具有一定的创新,关键是对题中“类”的题解,属于创新题,是中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
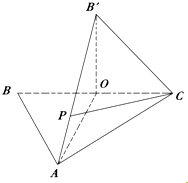 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B'点重合.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B'点重合.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
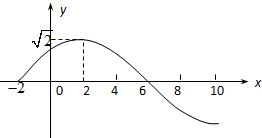 已知:函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示:
已知:函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com