
 用5种不同的颜色给如图中所给出的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,那么共有260种不同的涂色方法.
用5种不同的颜色给如图中所给出的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,那么共有260种不同的涂色方法. 分析 根据题意,先分析于1号区域,有5种颜色可选,即有5种涂法方案,再分①若2、3号区域涂不同的颜色,②若2、3号区域涂相同的颜色,两种情况讨论其他3个区域的涂色方案,由分类计数原理可得其他个区域的涂色方案的数目;再由分步计数原理计算可得答案.
解答 解:对于1号区域,有5种颜色可选,即有5种涂法,
分类讨论其他3个区域:①若2、3号区域涂不同的颜色,则有A42=12种涂法,4号区域有3种涂法,此时其他3个区域有12×3=36种涂法;
②若2、3号区域涂相同的颜色,则有4种涂法,4号区域有4种涂法,此时其他3个区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;
故答案为:260.
点评 本题考查分步计数原理与分类计数原理的综合运用,注意4个区域的位置关系即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | “φ=$\frac{π}{2}$”是“函数y=sin(2x+ϕ)为偶函数”的充要条件 | |
| B. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| C. | 命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | |
| D. | 当a<0时,幂函数y=xa在(0,+∞)上是单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
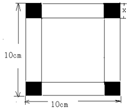 边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.
边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com