
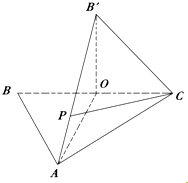
 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B'点重合.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B'点重合.分析 (1)证明AO⊥OB',AO⊥OC,然后证明AO⊥平面B'OC;
(2)在平面B'OC内,作B'D⊥OC于点D,当D与O重合时,三棱锥B'-AOC的体积最大,过O点作OH⊥B'C于点H,连AH,说明∠AHO即为二面角A-B'C-O的平面角.在三角形AOH中求解二面角A-B1C-O的余弦值.
(3)连接OP,说明OC⊥平面B'OA,CP与平面B'OA所成的角为∠CPO,证明CP⊥AB′,然后求解即可.
解答 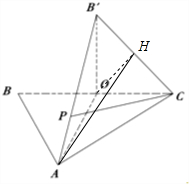 解:(1)证明:∵AB=AC且O是BC中点,
解:(1)证明:∵AB=AC且O是BC中点,
∴AO⊥BC即AO⊥OB',AO⊥OC,
又∵OB'∩OC=O,∴AO⊥平面B'OC;…(3分)
(2)在平面B'OC内,作B'D⊥OC于点D,
则由(Ⅰ)可知B'D⊥OA
又OC∩OA=O,∴B'D⊥平面OAC,
即B'D是三棱锥B'-AOC的高,
又B'D≤B'O,所以当D与O重合时,三棱锥B'-AOC的体积最大,
过O点作OH⊥B'C于点H,连AH,
由(Ⅰ)知AO⊥平面B'OC,
又B'C⊆平面B'OC,∴B'C⊥AO∵AO∩OH=O,∴B'C⊥平面AOH,
∴B'C⊥AH∴∠AHO即为二面角A-B'C-O的平面角.
在$R{t_{△AOH}}中,AO=2,OH=\frac{{\sqrt{2}}}{2}$,∴$AH=\frac{{3\sqrt{2}}}{2}$,
∴$cos∠AHO=\frac{OH}{AH}=\frac{1}{3}$,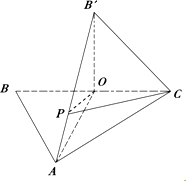
故二面角A-B1C-O的余弦值为$\frac{1}{3}$…(7分)
(3)连接OP,在(2)的条件下,易证OC⊥平面B'OA,
∴CP与平面B'OA所成的角为∠CPO,
∴$sin∠CPO=\frac{OC}{CP}=\frac{{\sqrt{5}}}{3}$∴$CP=\frac{3}{{\sqrt{5}}}$
又在△ACB′中,$sin∠A{B^'}C=\frac{{\frac{3}{{\sqrt{2}}}}}{{\sqrt{5}}}=\frac{3}{{\sqrt{10}}}=\frac{CP}{{\sqrt{2}}}$,
∴CP⊥AB′,
∴${B^'}P=\sqrt{{{({\sqrt{2}})}^2}-C{P^2}}=\frac{{\sqrt{5}}}{5}$,
∴$AP=\frac{{4\sqrt{5}}}{5}$…(12分)
点评 本题考查直线与平面垂直,二面角的平面镜以及直线与平面所成角,考查空间想象能力以及计算能力.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{15}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “φ=$\frac{π}{2}$”是“函数y=sin(2x+ϕ)为偶函数”的充要条件 | |
| B. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| C. | 命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | |
| D. | 当a<0时,幂函数y=xa在(0,+∞)上是单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com