
分析 (1)求出$\overrightarrow b$+$\overrightarrow c$,然后利用向量投影的定义,求解即可.
(2)表示出$\overrightarrow a$-t$\overrightarrow b$,通过向量与$\overrightarrow c$共线,列出方程求解即可.
解答 解:(1)$\overrightarrow b+\overrightarrow c=(5,0)$,
故$\overrightarrow a$在$\overrightarrow b+\overrightarrow c$上的投影为:$|\overrightarrow a|cos<\overrightarrow a,\overrightarrow b+\overrightarrow c>$=$\frac{\overrightarrow a•(\overrightarrow b+\overrightarrow c)}{|\overrightarrow b+\overrightarrow c|}=-3$…(4分)
(2)$\overrightarrow a-t\overrightarrow b=(-3-2t,2-t)$,$\overrightarrow a-t\overrightarrow b与\overrightarrow c$共线,
即:(-3-2t)×(-1)-(2-t)×3=0,
故$t=\frac{3}{5}$…(4分)
点评 本题考查向量数量积以及向量共线的充要条件的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{15}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
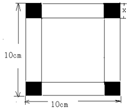 边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.
边长为10cm的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高茎 | 矮茎 | 合计 | |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com