
分析 (1)由题意知1,b为关于x的方程ax2-3x+2=0的两根,由韦达定理可得方程组,解出即可;
(2)将a,b的值代入不等式,求出不等式的解集即可.
解答 解:(1)由题意知1,b为关于x的方程ax2-3x+2=0的两根,
则 $\left\{\begin{array}{l}{b=\frac{2}{a}}\\{1+b=\frac{3}{a}}\end{array}\right.$,∴a=1,b=2.
(2)由(1)$\frac{x+3}{ax-b}$>0,
即$\frac{x+3}{x-2}$>0,解得:x>2或x<-3,
故不等式的解集是{x|x>2或x<-3}.
点评 该题考查一元二次不等式的解法,属基础题,深刻理解“三个二次”间的关系是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
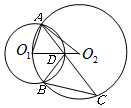 如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.
如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com