
分析 依题意知,a≤(x+$\frac{1}{x-1}$)min(x>1),利用基本不等式可求得x+$\frac{1}{x-1}$=(x-1)+$\frac{1}{x-1}$+1≥2$\sqrt{(x-1)•\frac{1}{x-1}}$+1=3,从而可得实数a的取值范围.
解答 解:因为当x>1时,不等式x+$\frac{1}{x-1}$≥a恒成立,
所以,a≤(x+$\frac{1}{x-1}$)min(x>1),
因为x>1时,x-1>0,
所以x+$\frac{1}{x-1}$=(x-1)+$\frac{1}{x-1}$+1≥2$\sqrt{(x-1)•\frac{1}{x-1}}$+1=3(当且仅当x-1=$\frac{1}{x-1}$,即x=2时取“=”),
所以,(x+$\frac{1}{x-1}$)min=3,
故a≤3,
故答案为:(-∞,3].
点评 本题考查函数恒成立问题,考查等价转化思想与基本不等式的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过四面体各面的垂心分别与各面垂直的直线交点为四面体外接球球心 | |
| B. | 过四面体各面的内心分别与各面垂直的直线交点为四面体外接球球心 | |
| C. | 过四面体各面的重心分别与各面垂直的直线交点为四面体外接球球心 | |
| D. | 过四面体各面的外心分别与各面垂直的直线交点为四面体外接球球心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
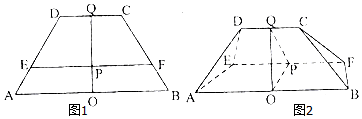
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com