
| A�� | �����������Ĵ��ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������� | |
| B�� | ���������������ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������� | |
| C�� | ���������������ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������� | |
| D�� | ���������������ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������� |
���� ���ƽ���������Ρ����ߴ�ֱƽ���ߵĽ��������������ԲԲ�ġ������ʣ�����֪���������������ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������ģ����ɵó����ۣ�
��� �⣺���ƽ���������Ρ����ߴ�ֱƽ���ߵĽ��������������ԲԲ�ġ������ʣ�����֪���������������ķֱ�����洹ֱ��ֱ�߽���Ϊ��������������ģ�
��ѡD��
���� ���⿼������������ؼ����ڷ�������ȣ����ܵõ���ȷ���ۣ����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �ٺ͢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
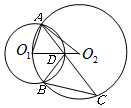 ��ͼ����֪��O1����O2�İ뾶�ֱ�Ϊr1��r2����O2������O1������Բ�ཻ�ڵ�A��B��CΪ��O2�ϵĵ㣬����AC����O1�ڵ�D��������BC��BD��AO1��AO2��O1O2�������ĸ����ۣ��١�BDC=��AO1O2����$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$��AD=DC ��BC=DC��������ȷ���۵����Ϊ�٢ڢܣ�
��ͼ����֪��O1����O2�İ뾶�ֱ�Ϊr1��r2����O2������O1������Բ�ཻ�ڵ�A��B��CΪ��O2�ϵĵ㣬����AC����O1�ڵ�D��������BC��BD��AO1��AO2��O1O2�������ĸ����ۣ��١�BDC=��AO1O2����$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$��AD=DC ��BC=DC��������ȷ���۵����Ϊ�٢ڢܣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com