
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)令g(x)=f(x)-kx=exsinx-kx,问题转化为当$x∈[0,\frac{π}{2}]$时,g(x)min≥0,根据函数的单调性求出k的范围即可;
(3)求出函数的导数,设出切点坐标,求出切线方程,根据三角函数的性质求出S的值即可.
解答 解:(1)∵$f'(x)={e^x}(sinx+cosx)=\sqrt{2}{e^x}sin(x+\frac{π}{4})$,
∴f(x)的增区间为$[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}]$(k∈Z);
减区间为$[2kπ+\frac{3π}{4},2kπ+\frac{7π}{4}]$(k∈Z).…(4分)
(2)令g(x)=f(x)-kx=exsinx-kx
要使f(x)≥kx恒成立,只需当$x∈[0,\frac{π}{2}]$时,g(x)min≥0,
∵g'(x)=ex(sinx+cosx)-k
令h(x)=ex(sinx+cosx),则h'(x)=2excosx≥0对$x∈[0,\frac{π}{2}]$恒成立,
∴h(x)在$[0,\frac{π}{2}]$上是增函数,则$h(x)∈[1,{e^{\frac{π}{2}}}]$,
①当k≤1时,g'(x)≥0恒成立,g(x)在$[0,\frac{π}{2}]$上为增函数,
∴g(x)min=g(0)=0,∴k≤1满足题意;
②当$1<k<{e^{\frac{π}{2}}}$时,g'(x)=0在$[0,\frac{π}{2}]$上有实根x0,h(x)在$[0,\frac{π}{2}]$上是增函数,
则当x∈[0,x0)时,g'(x)<0,∴g(x0)<g(0)=0不符合题意;
③当$k≥{e^{\frac{π}{2}}}$时,g'(x)≤0恒成立,g(x)在$[0,\frac{π}{2}]$上为减函数,
∴g(x)<g(0)=0不符合题意,∴k≤1,即k∈(-∞,1].…(8分)
(3)∵F(x)=f(x)+excosx=ex(sinx+cosx)∴F'(x)=2excosx,
设切点坐标为$({x_0},{e^{x_0}}(sin{x_0}+cos{x_0}))$,则切线斜率为$F'({x_0})=2{e^{x_0}}cos{x_0}$,
从而切线方程为$y-{e^{x_0}}(sin{x_0}+cos{x_0})=2{e^{x_0}}cos{x_0}(x-{x_0})$,
∴$-{e^{x_0}}(sin{x_0}+cos{x_0})=2{e^{x_0}}cos{x_0}(\frac{π-1}{2}-{x_0})$$?tan{x_0}=2({x_0}-\frac{π}{2})$,
令y1=tanx,${y_2}=2(x-\frac{π}{2})$,这两个函数的图象均关于点$(\frac{π}{2},0)$对称,
则它们交点的横坐标也关于$x=\frac{π}{2}$对称,
从而所作的所有切线的切点的横坐标构成数列{xn}的项也关于$x=\frac{π}{2}$成对出现,
又在$[-\frac{2015π}{2},\frac{2017π}{2}]$共有1008对,每对和为π.
∴S=1008π.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查三角函数的性质以及转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
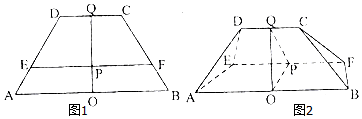
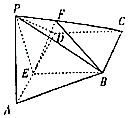 如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.
如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com