
分析 构造g(x)=f(x)-2=sinx+aln|1-$\frac{2}{x+1}$|,从而证明函数为奇函数,从而求得.
解答 解:令g(x)=f(x)-2=sinx+aln|1-$\frac{2}{x+1}$|,
g(-x)=sin(-x)+aln|1-$\frac{2}{-x+1}$|
=-sinx-aln|$\frac{-x+1}{-x-1}$|
=-sinx-aln|1-$\frac{2}{x+1}$|=-g(x),
g($\frac{π}{6}$)=f($\frac{π}{6}$)-2=4-2=2,
故g(-$\frac{π}{6}$)=f(-$\frac{π}{6}$)-2=-2,
故f(-$\frac{π}{6}$)=0,
故答案为:0.
点评 本题考查了函数的性质的判断与应用,同进考查了转化与整体思想的应用及构造法的应用.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
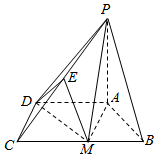 已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.
已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com