
���� ��1��������õ������ַ����Ļ������������ڸ��������µĸ��ʣ�д����������ķֲ��У�������������軯����������������������軯������ĸ��ʣ�
��2��������һ���ҵĻ�������ķֲ��У������������㹫ʽ�õ������
��� �⣺��������������ʱ�������ֿ��ܣ�
��������ֻ���Ϊ���ԣ��ٴ��������ʱ��ǡ��һ�����и���Ϊ��$\frac{{∁}_{4}^{2}{A}_{3}^{3}}{{A}_{5}^{3}}$��$\frac{1}{{A}_{3}^{1}}$=$\frac{1}{5}$��
��������ֻ���Ϊ���ԣ��ٴ�������ֻ��������ԣ����۵ڶ�����������û�У��������ڵڶ��ν�������
$\frac{{A}_{4}^{3}}{{A}_{5}^{3}}•\frac{{A}_{2}^{1}}{{A}_{2}^{2}}$=$\frac{2}{5}$��
����ֻ�����εĸ���Ϊ$\frac{1}{5}+\frac{2}{5}$=$\frac{3}{5}$��
����������ʱ��ֻ��һ�ֿ��ܣ�
������ֻ���Ϊ���ԣ��ٴ��������ʱ��ǡ�ö������и���Ϊ���������ʱ����Ϊ$\frac{2}{5}$��
����ַ����Ĵ������������ִ����ĸ���Ϊ��$\frac{3}{5}$��$��1-\frac{1}{5}��$+$\frac{2}{5}����1-\frac{1}{5}-\frac{1}{5}��$=$\frac{18}{25}$��
���α�ʾ�����������軯�������
��ε�����ΪE��=2��0.6+3��0.4=2.4��
���� ���⿼����������뻥���¼��ĸ��ʼ��㹫ʽ����������ķֲ��м�����ѧ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
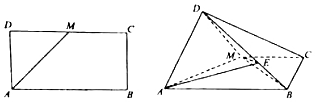
 ��ͼ��ʾΪһ��Ի��ǵ�¡��ļ����壬��֪AE�͵���BCFE��DF��AE��DF=AE=1��CE=$\sqrt{7}$���ı���ABCD�������Σ�
��ͼ��ʾΪһ��Ի��ǵ�¡��ļ����壬��֪AE�͵���BCFE��DF��AE��DF=AE=1��CE=$\sqrt{7}$���ı���ABCD�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
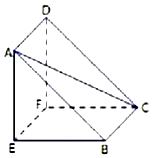
 ��ͼ����������ABC-A1B1C1�У�AB��ƽ��BB1C1C�����ı���BB1C1C�����Σ���BCC1=60�㣮
��ͼ����������ABC-A1B1C1�У�AB��ƽ��BB1C1C�����ı���BB1C1C�����Σ���BCC1=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$�����Ҷ���ֱ�ΪA1��A2�����ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$����B��4��0����F2Ϊ�߶�A1B���е㣮
��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$�����Ҷ���ֱ�ΪA1��A2�����ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$����B��4��0����F2Ϊ�߶�A1B���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com