
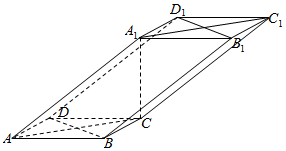
 如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.
如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.分析 (I)由A1C⊥底面ABCD得A1C⊥BD,由菱形性质得AC⊥BD,故BD⊥平面ACC1A1,从而平面ACC1A1⊥平面DBB1D1.
(II)连结上下底面中心O1O,过A1作A1F⊥O1O,则A1F⊥平面DBB1D1.设A1与O1O的交点为E,于是∠A1EF为直线A1C与平面DBB1D1所成的角.根据等边三角形性质求出OC,OE解出∠OEC即∠A1EF的大小.
解答 (I)证明:∵ABCD是菱形,∴AC⊥BD ,
,
又∵A1C⊥底面ABCD,BD?平面ABCD,
∴A1C⊥BD,
又AC?平面ACC1A1,A1C?平面ACC1A1,AC∩A1C=C,
∴BD⊥面ACC1A1,而BD∈面DBB1D1,
∴面ACC1A1⊥面DBB1D1.
(II)解:设四棱柱上下底面中心分别是O1、O,连接O1O,
则四边形ACC1A1为平行四边形,设O1O与A1C的交点为E,过A1作A1⊥FO1O于F,
∵平面ACC1A1⊥平面DBB1D1,平面ACC1A1∩面DBB1D1=O1O,A1F⊥O1O,A1F?面ACC1A1,
∴A1F⊥面DBB1D1.
∴∠A1EF为直线A1C与平面DBB1D1所成的角.
∵底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,
∴OC=$\frac{1}{2}$AC=$\sqrt{3}$,∠A1CA=90°,OE=$\frac{1}{2}$AA1=2,
∴$sin∠OEC=\frac{OC}{OE}=\frac{{\sqrt{3}}}{2}$,∴∠OEC=60°.
∴∠A1EF=∠OEC=60°.
∴直线A1C与面DBB1D1所成角为60°.
点评 本题考查了面面垂直的判定,线面角的计算,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | 12π | C. | 6$\sqrt{3}$π | D. | 6$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | -$\frac{1}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
2015年,威海智慧公交建设项目已经基本完成.为了解市民对该项目的满意度,分别从不同公交站点随机抽取若干市民对该项目进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com