
| A. | 6π | B. | 12π | C. | 6$\sqrt{3}$π | D. | 6$\sqrt{2}$π |
分析 利用直线平面的垂直得出BD⊥BC,AD⊥AC利用直角三角形的性质得出球心,即可求解外接球的半径.
解答 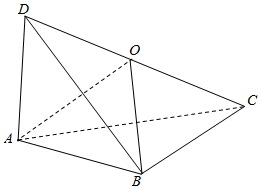 解:∵AB=BC=AD=$\sqrt{2}$,BD=AC=2,BC⊥AD,
解:∵AB=BC=AD=$\sqrt{2}$,BD=AC=2,BC⊥AD,
∴AB2+BC2=AC2,AD2+AB2=BD2,
AB⊥BC,AD⊥AB,
∵BC∩AB=C,AB∩BC=B,
∴BC⊥面ABD,AD⊥面ABC,
∵BD?面ABD,AC?面ACB;
∴BD⊥BC,AD⊥AC,
∵O为DC中点,
∴直角三角形中得出:OA=OB=OC=OD,
O 为外接球的球心,
半径R=$\frac{1}{2}×\sqrt{{2}^{2}+(\sqrt{2})^{2}}$=$\frac{\sqrt{6}}{2}$,
∴三棱锥D-ABC外接球的表面积为:4π×($\frac{\sqrt{6}}{2}$)2=6π,
故选:A.
点评 本题综合考查了直线平面的垂直的判断性质定理,综合运用平面知识解决空间问题的能力.


科目:高中数学 来源: 题型:解答题
| 类型 | A类 | B类 | C类 |
| 已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
| 已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品编号 | ① | ② | ③ | ④ | ⑤ |
| 电压(x) | 10 | 15 | 20 | 25 | 30 |
| 电流(y) | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
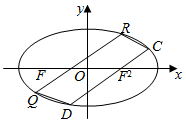 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
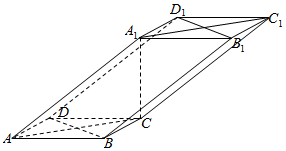 如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.
如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com