
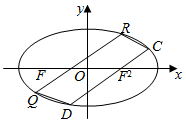
 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.分析 (Ⅰ)设F2(c,0),令x=c,代入椭圆方程,可得弦长为3,再将R的坐标代入椭圆方程,解方程可得a=2,b=$\sqrt{3}$,c=1,即有抛物线的焦点,进而椭圆方程和抛物线的方程;
(Ⅱ)设P(t2,2t)(t≠0),设抛物线切线l的方程为y-2t=k(x-t2),对抛物线的方程两边对x求导,可得切线的斜率,即可得到切线的方程,代入椭圆方程,运用韦达定理和弦长公式,点到直线的距离公式,由三角形的面积公式和换元法,运用对勾函数的单调性和二次函数的最值求法,可得三角形的面积的最大值;
(Ⅲ)可设直线l1:y=m(x-1),代入椭圆方程,运用韦达定理,再由直线RQ:y=m(x-1)+$\frac{3}{2}$,代入椭圆方程,运用韦达定理可得Q的坐标,假设四边形RQCD的对角线互相平分,可得四边形RQCD为平行四边形,RD与QC的中点重合.运用中点坐标公式,结合韦达定理,解方程可得m,进而得到所求直线的方程.
解答 解:(Ⅰ)设F2(c,0),令x=c,代入椭圆方程可得,
y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=±$\frac{{b}^{2}}{a}$,
由题意可得$\frac{2{b}^{2}}{a}$=3,
又R(1,$\frac{3}{2}$)在椭圆上,可得$\frac{1}{{a}^{2}}$+$\frac{9{b}^{2}}{4}$=1,
解得a=2,b=$\sqrt{3}$,c=1,
可得椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
即有抛物线的焦点为(1,0),
可得抛物线C2的方程为y2=4x;
(Ⅱ)设P(t2,2t)(t≠0),设抛物线切线l的方程为y-2t=k(x-t2),
由y2=4x两边对x求导,可得2yy′=4,即为y′=$\frac{2}{y}$,
可得k=$\frac{2}{2t}$=$\frac{1}{t}$,即有切线l的方程为t(y-2t)=x-t2,
即为x=ty-t2,代入椭圆方程3x2+4y2=12,
可得(4+3t2)y2-6t3y+3t4-12=0,
设A(x1,y1),B(x2,y2),
即有△=36t6-12(4+3t2)(t4-4)>0,得0<t2<4,
y1+y2=$\frac{6{t}^{3}}{4+3{t}^{2}}$,y1y2=$\frac{3{t}^{4}-12}{4+3{t}^{2}}$,
|AB|=$\sqrt{1+{t}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+{t}^{2}}$•$\sqrt{\frac{36{t}^{6}}{(4+3{t}^{2})^{2}}-\frac{4(3{t}^{4}-12)}{4+3{t}^{2}}}$
=4$\sqrt{3}$•$\sqrt{1+{t}^{2}}$•$\sqrt{\frac{-{t}^{4}+3{t}^{2}+4}{(4+3{t}^{2})^{2}}}$,
原点到直线l的距离为d=$\frac{{t}^{2}}{\sqrt{1+{t}^{2}}}$,
则△AOB面积S=$\frac{1}{2}$|AB|•d=2$\sqrt{3}$t2•$\sqrt{\frac{-{t}^{4}+3{t}^{2}+4}{(4+3{t}^{2})^{2}}}$,
令u=4+3t2,0<t2<4,可得4<u<16,
则S=$\frac{2\sqrt{3}}{9}$•$\sqrt{\frac{({u}^{2}-8u+16)(-{u}^{2}+17u-16)}{{u}^{2}}}$=$\frac{2\sqrt{3}}{9}$•$\sqrt{(u+\frac{16}{u}-8)(17-u-\frac{16}{u})}$,
可令v=u+$\frac{16}{u}$,由4<u<16,可得v=u+$\frac{16}{u}$在(4,16)递增,
可得8<v<17,即有S=$\frac{2\sqrt{3}}{9}$•$\sqrt{-{v}^{2}+25v-136}$,
即有当v=$\frac{25}{2}$∈(8,17)时,S取得最大值$\frac{2\sqrt{3}}{9}$•$\sqrt{-\frac{625}{4}+\frac{625}{2}-136}$=$\sqrt{3}$.
由u+$\frac{16}{u}$=$\frac{25}{2}$,解得u=$\frac{25+3\sqrt{41}}{4}$,t=$\frac{\sqrt{3+\sqrt{41}}}{2}$<2,
故当t=$\frac{\sqrt{3+\sqrt{41}}}{2}$时,△AOB的面积取得最大值$\sqrt{3}$;
(Ⅲ)可设直线l1:y=m(x-1),代入椭圆3x2+4y2=12,
可得(3+4m2)x2-8m2x+4m2-12=0,
设C(x1,y1),D(x2,y2),可得
x1+x2=$\frac{8{m}^{2}}{3+4{m}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{m}^{2}}$,
直线RQ:y=m(x-1)+$\frac{3}{2}$,代入椭圆3x2+4y2=12,
可得(3+4m2)x2+(12-8m)mx+4m2-12m-3=0,
设Q(x3,y3),可得
x3+1=$\frac{m(8m-12)}{3+4{m}^{2}}$,x3•1=$\frac{4{m}^{2}-12m-3}{3+4{m}^{2}}$,
假设四边形RQCD的对角线互相平分,可得四边形RQCD为平行四边形,
RD与QC的中点重合.
即有$\frac{{x}_{2}+1}{2}$=$\frac{{x}_{3}+{x}_{1}}{2}$,即为x1-x2=1-x3,
即有(x1-x2)2=(x1+x2)2-4x1x2=(1-x3)2,
则有($\frac{8{m}^{2}}{3+4{m}^{2}}$,)2-$\frac{4(4{m}^{2}-12)}{3+4{m}^{2}}$=(1-$\frac{4{m}^{2}-12m-3}{3+4{m}^{2}}$)2,
即为$\frac{16(9+9{m}^{2})}{(3+4{m}^{2})^{2}}$=$\frac{(6+12m)^{2}}{(3+4{m}^{2})^{2}}$,
解得m=$\frac{3}{4}$.
故存在直线l1,方程为y=$\frac{3}{4}$x-$\frac{3}{4}$.
点评 本题考查椭圆和抛物线的方程的求法,注意运用点满足椭圆方程,考查三角形的面积的最大值,注意运用直线方程和椭圆方程联立,运用韦达定理和弦长公式,以及点到直线的距离公式,考查存在性问题的解法,同时考查对勾函数的单调性和二次函数的最值求法,考查化简整理的运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路l的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | 12π | C. | 6$\sqrt{3}$π | D. | 6$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.
如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | -$\frac{1}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com