
分析 (1)第2局中可能是乙当裁判,其概率为$\frac{1}{3}$,也可能是丙当裁判,其概率为$\frac{2}{3}$,由此能求出第3局甲当裁判的概率.
(2)由题意X可能的取值为0,1,2,分别求出相应的概率,由此能求出X的概率分布与数学期望.
解答 解:(1)第2局中可能是乙当裁判,其概率为$\frac{1}{3}$,
也可能是丙当裁判,其概率为$\frac{2}{3}$,
∴第3局甲当裁判的概率为$\frac{1}{3}×\frac{2}{3}+\frac{2}{3}×\frac{1}{3}$=$\frac{4}{9}$.…(4分)
(2)由题意X可能的取值为0,1,2.…(5分)
P(X=0)=$\frac{2}{3}×\frac{1}{2}×\frac{2}{3}$=$\frac{2}{9}$,…(6分)
P(X=1)=$\frac{1}{3}×(\frac{1}{3}×\frac{2}{3}+\frac{2}{3}×\frac{1}{2})+\frac{2}{3}×\frac{1}{2}+\frac{2}{3}×\frac{1}{2}×\frac{1}{3}$=$\frac{17}{27}$,…(7分)
P(X=2)=$\frac{1}{3}×(\frac{2}{3}×\frac{1}{2}+\frac{1}{3}×\frac{1}{3})$=$\frac{4}{27}$.…(8分)
∴X的概率分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{2}{9}$ | $\frac{17}{27}$ | $\frac{4}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [10,25) | [25,40) | [40,55] |
| 成绩优秀 | 670 | a | b |
| 成绩一般 | 80 | 60 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品编号 | ① | ② | ③ | ④ | ⑤ |
| 电压(x) | 10 | 15 | 20 | 25 | 30 |
| 电流(y) | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
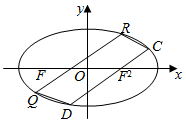 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右两个焦点分别为F1,F2,R(1,$\frac{3}{2}$)为椭圆C1上一点,过F2且与x轴垂直的直线与椭圆C1相交所得弦长为3.抛物线C2的顶点是椭圆C1的中心,焦点与椭圆C1的右焦点重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com