
分析 运用分析法证明,要证原不等式成立,可通过两边平方,化简整理,再由配方即可得证.
解答 证明:由a+b=1,(a+$\frac{1}{2}$)(b+$\frac{1}{2}$)≥0,
可得a+$\frac{1}{2}$≥0,b+$\frac{1}{2}$≥0,
要证$\sqrt{a+\frac{1}{2}}$+$\sqrt{b+\frac{1}{2}}$≤2,
两边平方即证a+b+1+2$\sqrt{(a+\frac{1}{2})(b+\frac{1}{2})}$≤4,
即为$\sqrt{(a+\frac{1}{2})(b+\frac{1}{2})}$≤1,
再两边平方可得(a+$\frac{1}{2}$)(b+$\frac{1}{2}$)≤1,
展开即为ab+$\frac{1}{2}$(a+b)+$\frac{1}{4}$≤1,代入a+b=1,
可得ab≤$\frac{1}{4}$,即有a(1-a)-$\frac{1}{4}$≤0,
即为-(a-$\frac{1}{2}$)2≤0,显然成立.
则原不等式成立.
点评 本题考查不等式的证明,运用了分析法证明,这是常用方法,本题也可运用柯西不等式:(ac+bd)2≤(a2+b2)(c2+d2),考查推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类型 | A类 | B类 | C类 |
| 已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
| 已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [10,25) | [25,40) | [40,55] |
| 成绩优秀 | 670 | a | b |
| 成绩一般 | 80 | 60 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品编号 | ① | ② | ③ | ④ | ⑤ |
| 电压(x) | 10 | 15 | 20 | 25 | 30 |
| 电流(y) | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
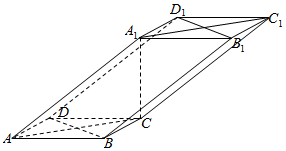 如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.
如图,在四棱柱ABCD-A1B1C1D1,底面ABCD是边长为2的菱形,∠BAD=60°,AA1=4,且A1C⊥底面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com