
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点.分析 (Ⅰ)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能证明AF⊥EC.
(Ⅱ)求出$\overrightarrow{MN}$=($\frac{1}{2}$,-$\frac{1}{2},\frac{1}{2}$),$\overrightarrow{AE}$=(-1,0,1),$\overrightarrow{AF}$=(0,1,1),利用向量法能证明MN⊥平面AEF.
(Ⅲ)求出平面AEF的法向量和平面CEF的法向量,利用向量法能求出二面角A-EF-C的余弦值.
解答 证明:(Ⅰ)∵四边形ABCD是边长为1的正方形,ED⊥平面ABCD,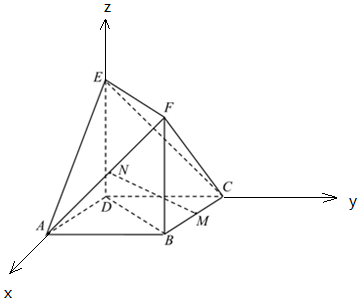
∴以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
∵FB⊥平面ABCD,且ED=FB=1,M为BC的中点,N为AF的中点,
∴A(1,0,0),F(1,1,1),E(0,0,1),C(0,1,0),
$\overrightarrow{AF}$=(0,1,1),$\overrightarrow{EC}$=(0,1,-1),
∴$\overrightarrow{AF}•\overrightarrow{EC}$=0+1-1=0,
∴AF⊥EC.
(Ⅱ)M($\frac{1}{2}$,1,0),N(1,$\frac{1}{2},\frac{1}{2}$),
$\overrightarrow{MN}$=($\frac{1}{2}$,-$\frac{1}{2},\frac{1}{2}$),$\overrightarrow{AE}$=(-1,0,1),$\overrightarrow{AF}$=(0,1,1),
∵$\overrightarrow{MN}•\overrightarrow{AE}$=-$\frac{1}{2}+0+\frac{1}{2}$=0,$\overrightarrow{MN}•\overrightarrow{AF}$=0-$\frac{1}{2}+\frac{1}{2}$=0,
∴$\overrightarrow{MN}$⊥$\overrightarrow{AE}$,$\overrightarrow{MN}$⊥$\overrightarrow{AF}$,∴MN⊥AE,MN⊥AF,
∵AE∩AF=A,∴MN⊥平面AEF.
解:(Ⅲ)$\overrightarrow{CE}$=(0,-1,1),$\overrightarrow{CF}$=(1,0,1),
设平面AEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=-x+z=0}\\{\overrightarrow{n}•\overrightarrow{AF}=y+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-1,1),
设平面CEF的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CE}=-b+c=0}\\{\overrightarrow{m}•\overrightarrow{CF}=a+c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,-1,-1),
设二面角A-EF-C的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{3}•\sqrt{3}}$=$\frac{1}{3}$.
∴二面角A-EF-C的余弦值为$\frac{1}{3}$.
点评 本题考查线线垂直、线面垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(1,+∞),x3+16≤8x | B. | ¬p:?x∈(1,+∞),x3+16<8x | ||
| C. | ¬p:?x0∈(1,+∞),x03+16≤8x0 | D. | ¬p:?x0∈(1,+∞),x03+16<8x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
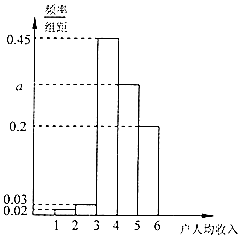 我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.
我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
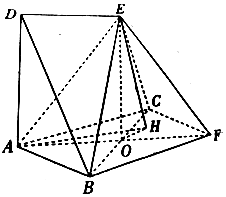 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (3,0) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{3}$,-$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
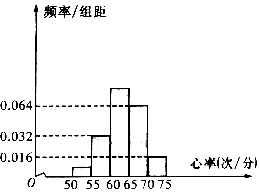 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com