Question

15．A，B，C为圆O上三点，且直线OC与直线AB交于圆外一点，若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$，则m+n的范围是（　　）

• A． （0，1）
• B． （1，+∞）
• C． （-1，0）
• D． （-∞，-1）

Answer 1

分析 可设直线OC与直线AB交于点D，这样画出图形，从而可得出$\overrightarrow{OD}=k\overrightarrow{OC}$，并得到k＞1，进而得出$\overrightarrow{OD}=km\overrightarrow{OA}+kn\overrightarrow{OB}$，由A，B，D三点共线即可得到km+kn=1，这样根据k的范围，即可求出m+n的范围．

解答 解：如图，设直线OC与直线AB交于D，则：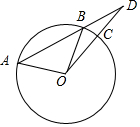
$\overrightarrow{OD}=k\overrightarrow{OC}$，且k＞1；
又$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$；
∴$\overrightarrow{OD}=km\overrightarrow{OA}+kn\overrightarrow{OB}$，且A，B，D三点共线；
∴km+kn=1；
∴$m+n=\frac{1}{k}$，k＞1；
∴0＜m+n＜1；
即m+n的范围是（0，1）．
故选A．

点评 考查共线向量基本定理，向量数乘的几何意义，以及三点共线的充要条件，不等式的性质．