
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\sqrt{2}-1,1)$ | C. | $[\sqrt{2}-1,1)$ | D. | $(0,\sqrt{2}-1]$ |
分析 由正弦定理及椭圆的离心率公式可知:椭圆的离心率e=$\frac{c}{a}$=$\frac{sin∠P{F}_{2}{F}_{1}}{sin∠P{F}_{1}{F}_{2}}$,$\frac{丨P{F}_{1}丨}{丨P{F}_{2}丨}$=e,作出椭圆的左准线l,作PQ⊥l于Q,根据椭圆的第二定义得|PQ|=|PF2|=$\frac{丨P{F}_{1}丨}{e}$.设P(x,y),将|PF1|、|PF2|表示为关于a、c、e、x的式子,利用|PF2|+|PF1|=2a,解出x═$\frac{ae-a}{e(e+1)}$.最后根据椭圆上点的横坐标满足-a≤x≤a,建立关于e的不等式并解得e<-1-$\sqrt{2}$或e>$\sqrt{2}$,根据椭圆离心率的取值范围,即可得到该椭圆离心率的取值范围.
解答 解: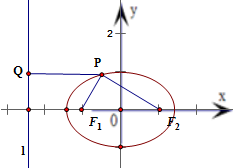 ∵△PF1F2中,由正弦定理得$\frac{丨P{F}_{1}丨}{sin∠P{F}_{2}{F}_{1}}$=$\frac{丨P{F}_{2}丨}{sin∠P{F}_{1}{F}_{2}}$,
∵△PF1F2中,由正弦定理得$\frac{丨P{F}_{1}丨}{sin∠P{F}_{2}{F}_{1}}$=$\frac{丨P{F}_{2}丨}{sin∠P{F}_{1}{F}_{2}}$,
∴$\frac{丨P{F}_{1}丨}{丨P{F}_{2}丨}$=$\frac{sin∠P{F}_{2}{F}_{1}}{sin∠P{F}_{1}{F}_{2}}$.
又∵csin∠PF1F2=asin∠PF2F1,
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{sin∠P{F}_{2}{F}_{1}}{sin∠P{F}_{1}{F}_{2}}$,由此可得$\frac{丨P{F}_{1}丨}{丨P{F}_{2}丨}$=e,
作出椭圆的左准线l,设P在l上的射影为点Q,连结PQ,
由椭圆的第二定义,得$\frac{丨P{F}_{1}丨}{丨PQ丨}$=e,
因此|PQ|=|PF2|=$\frac{丨P{F}_{1}丨}{e}$.
设P(x,y),可得|PQ|=x+$\frac{{a}^{2}}{c}$,
∴|PF2|=x+$\frac{{a}^{2}}{c}$,|PF1|=e|PF2|=e(x+$\frac{{a}^{2}}{c}$).
由椭圆的第一定义,得|PF2|+|PF1|=2a,即(1+e)(x+$\frac{{a}^{2}}{c}$)=2a,解得x=$\frac{2a}{1+e}$-$\frac{{a}^{2}}{c}$=$\frac{ae-a}{e(e+1)}$.
∵P(x,y)为椭圆上一点,满足-a<x<a,
∴-a<$\frac{ae-a}{e(e+1)}$<a,即-1<$\frac{e-1}{e(e+1)}$<1,
解得e<-1-$\sqrt{2}$或e>$\sqrt{2}$,
∵椭圆的离心率e∈(0,1),
∴该椭圆离心率的取值范围是($\sqrt{2}$-1,1).
故选B.
点评 本题考查椭圆的第二定义的应用,考查离心率的取值范围.着重考查了正弦定理、椭圆的定义与简单几何性质和不等式的解法等知识,属于难题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:填空题
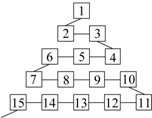 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com