
分析 (1)由解析式先求出函数的定义域,化简f(x)和f(-x)后,由函数奇偶性的定义即可证明;
(2)根据函数单调性的定义:取值、作差、变形、定号、下结论,进行证明即可.
解答 (1)证明:f(x)的定义域为{x|x≠0},关于原点对称,
∵f(1)=2,∴1+a=2,即a=1
∵f(x)=$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$,f(-x)=-x-$\frac{1}{x}$=-f(x),
∴f(x)是奇函数.
(2)证明:任取x1,x2∈(1,+∞)且x1<x2,
∴f(x1)-f(x2)=x1+$\frac{1}{x1}$-(x2+$\frac{1}{x2}$)
=(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$.
∵x1<x2,且x1x2∈(1,+∞),
∴x1-x2<0,x1x2>1,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(1,+∞)上为增函数.
点评 本题考查函数奇偶性的定义,函数单调性的定义:取值、作差、变形、定号、下结论的应用,考查化简、变形能力,属于中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\sqrt{2}-1,1)$ | C. | $[\sqrt{2}-1,1)$ | D. | $(0,\sqrt{2}-1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
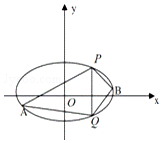 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-1 | D. | -$\frac{\sqrt{3}}{2}$或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | [-2,1] | C. | {-2,-1,0} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com