
分析 由题意知BAA-1=EA-1⇒B=A-1,所以矩阵B的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{-3}&{λ-2}\end{array}|$=λ2-3λ-4;
解答 解:∵BA=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,∴BAA-1=EA-1⇒B=A-1;
∵A-1=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$,∴B=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$;
∴矩阵B的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{-3}&{λ-2}\end{array}|$=λ2-3λ-4;
由f(λ)=0,解得λ1=-1,λ2=4;
∴矩阵B的特征值为-1和4.
点评 本题主要考查了矩阵与逆矩阵之间的关系,以及特征多项式的求法,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
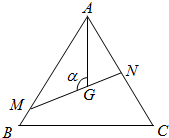 如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在($\frac{1}{2}$,+∞)内是增函数 | B. | f(x)在($\frac{1}{2}$,+∞)内是减函数 | ||
| C. | f(x)在(-∞,$\frac{1}{2}$)内是增函数 | D. | f(x)在(-∞,$\frac{1}{2}$)内是减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com