
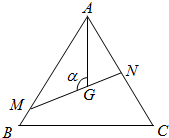
 如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.分析 (Ⅰ)由三角形重心的性质可得AG,再由正弦定理求得∠AMG,则答案可求;
(Ⅱ)由正弦定理把MG、NG用含有α的三角函数表示,代入面积公式可得S1,S2关于α的函数;
(Ⅲ)把(Ⅱ)中的函数式代入,化简后放缩得答案.
解答 解:(Ⅰ)∵△ABC边长为1的正三角形,G为△ABC的重心,
∴$AG=\frac{2}{3}AD$=$\frac{\sqrt{3}}{3}$,在△AMG中,$α=\frac{2π}{3}$,∠MAG=$\frac{π}{6}$,∴$∠AMG=\frac{π}{6}$,
∴MG=AG=$\frac{\sqrt{3}}{3}$;
(Ⅱ)在△AMG中,∠MAG=$\frac{π}{6}$,∴∠AMG=$\frac{5π}{6}-α$,
由正弦定理可得:$MG=\frac{AG}{sin(\frac{5π}{6}-α)}sin\frac{π}{6}=\frac{\sqrt{3}}{6sin(\frac{5π}{6}-α)}$,
在△ANG中,同理可得NG=$\frac{\sqrt{3}}{6sin(α-\frac{π}{6})}$,
∴${S}_{1}=\frac{1}{2}|MG|•|AG|•sinα=\frac{sinα}{12sin(α+\frac{π}{6})}$;
${S}_{2}=\frac{1}{2}|NG|•|AG|•sin(π-α)=\frac{sinα}{12(α-\frac{π}{6})}$.
(Ⅲ)由$\frac{π}{3}$≤α≤$\frac{2π}{3}$,得$\frac{{\sqrt{3}}}{2}≤sinα≤1$,
$y=\frac{1{2}^{2}}{si{n}^{2}α}[si{n}^{2}(α+\frac{π}{6})+si{n}^{2}(α-\frac{π}{6})]$=$144(1+\frac{1}{2si{n}^{2}α})≥144(1+\frac{1}{2})=216$,
当且仅当$α=\frac{π}{2}$时,y的最小值为216.
点评 本题考查在实际问题中建立三角函数模型,考查正弦定理的应用,考查计算能力,是中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33 | B. | 30 | C. | 31 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 24π | C. | 16π | D. | 32π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com