已知x＜0.求$y=\frac{{1+{x^2}}}{x}$的最大值=-2．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

16．已知x＜0，求$y=\frac{{1+{x^2}}}{x}$的最大值=-2．

分析根据基本不等式的性质求出y的最大值即可．

解答解：∵x＜0，
∴$y=\frac{{1+{x^2}}}{x}$=x+$\frac{1}{x}$≤-2$\sqrt{（-x）•（-\frac{1}{x}）}$=-2，
故答案为：-2．

点评本题考查了基本不等式的性质，注意应用性质的条件，本题是一道基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

6．

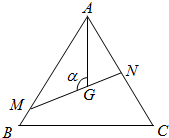如图，是△ABC边长为1的正三角形，M，N分别是AB，AC边上的点，线段MN过△ABC的重心，设∠MGA=α，$\frac{π}{3}$≤α≤$\frac{2π}{3}$．
（Ⅰ）当α=$\frac{2π}{3}$时，求MG的长；
（Ⅱ）分别记△AGM，△AGN的面积为S₁，S₂，试将S₁，S₂表示为α的函数；
（Ⅲ）设y=$\frac{1}{{{S}_{1}}^{2}}$+$\frac{1}{{{S}_{2}}^{2}}$，求y的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．各项均为正数的数列{a_n}中，前n项和${S_n}={（{\frac{{{a_n}+1}}{2}}）^2}$．
（1）求数列{a_n}的通项公式；
（2）若$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$＜k恒成立，求k的取值范围；
（3）是否存在正整数m，k，使得a_m，a_m+5，a_k成等比数列？若存在，求出m和k的值，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

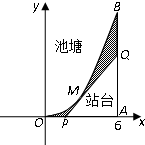如图，池塘的边缘为曲线段OMB，它可以近似看成是函数f（x）=x²在0≤x≤6的图象，BA垂直于x轴于点A，现要建一个以A为直角的观光站台△APQ，其中斜边PQ与曲线段OMB相切于点M（t，t²），切线PQ交x轴于点P，交线段AB于点Q，图中的阴影部分种植草坪．
（1）将△QAP的面积表达为t的函数；
（2）求草坪的面积的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．已知函数f（x）=sin（x+$\frac{7π}{4}$）+cos（x-$\frac{3π}{4}$），x∈R．
（1）求f（x）的最小正周期和最小值；
（2）已知f（α）=$\frac{6}{5}$，0＜α＜$\frac{3π}{4}$，求f（2α）的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．

如图，在三棱柱ABC-A₁B₁C₁中，A₁A⊥平面ABC，∠BAC=90°，F为棱AA₁上的动点，A₁A=4，AB=AC=2．
（1）当F为A₁A的中点，求直线BC与平面BFC₁所成角的余弦值；
（2）当$\frac{AF}{{F{A_1}}}$的值为多少时，二面角B-FC₁-C的大小是45°．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．关于函数f（x）=log${\;}_{\frac{1}{2}}$（1-2x）的单调性，叙述正确的是（　　）

	A．	f（x）在（$\frac{1}{2}$，+∞）内是增函数		B．	f（x）在（$\frac{1}{2}$，+∞）内是减函数
	C．	f（x）在（-∞，$\frac{1}{2}$）内是增函数		D．	f（x）在（-∞，$\frac{1}{2}$）内是减函数

查看答案和解析>>

科目：高中数学 来源： 题型：解答题