
| A. | 8π | B. | 24π | C. | 16π | D. | 32π |
分析 三棱锥的体积为Vp-ABC=$\frac{1}{3}$×PA×S△ABC,要使Vp-ABC取得最大,则S△ABC 取最大值;
又由于AB2+BC2≥2AB•BC⇒AB•BC≤4,当且仅当AB=BC时取最大值,S△ABC 的最大值为2;
所以,△ABC为等腰直角三角形,则球心O所在直线垂直过AC线段中心M,且与PA平行,即可判断球心位置.
解答 解:由题意知,PA⊥平面ABC,且PA=4;
三棱锥的体积为Vp-ABC=$\frac{1}{3}$×PA×S△ABC,
要使Vp-ABC取得最大,则S△ABC 取最大值;
∵∠ABC=90°,AC=2$\sqrt{2}$;
∵AB2+BC2≥2AB•BC⇒AB•BC≤4;
∴S△ABC 的最大值为$\frac{1}{2}$×4=2,当且仅当AB=BC时取最大值;
所以,△ABC为等腰直角三角形,
则球心O所在直线垂直过AC线段中心M,且与PA平行;
∵AC=2$\sqrt{2}$⇒AM=$\sqrt{2}$;
设球半径为R,则OA=OP,OM=2;
由勾股定理知:R2=$(\sqrt{2})^{2}$+22⇒R=$\sqrt{6}$;
外接球表面积为S=4πR2=24π;
故选:B.
点评 本题主要考查了三棱锥的体积求法,函数最值问题以及分析球心位置,属中等题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
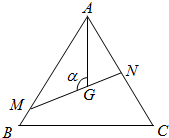 如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
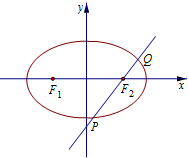 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
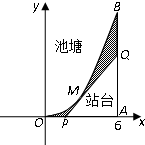 如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪.
如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com