
分析 (1)根据从2016年开始到2025年每年人口比上年增加0.5万人,从2026年开始到2035年每年人口为上一年的99%,可得分段函数;
(2)从2016年到2035年共20年,由等差数列及等比数列的求和公式,可求S20,从而可得新政策实施到2035年年人口均值,即可得出结论.
解答 解:(1)当n≤10时,数列{an}是首项为45.5,公差为0.5的等差数列,
∴an=45.5+0.5×(n-1)=45+0.5n …(2分)
当n≥11时,数列{an}是以公比为0.99的等比数列,又an=50
∴an=50×0.99n-10 …(4分)
因此,新政策实施后第n年的人口总数an(单位:万元)的表达式为
an=$\left\{\begin{array}{l}{45+0.5n,1≤n≤10}\\{50×0.9{9}^{n-10},11≤n≤20}\end{array}\right.$ …(6分)
(2)设Sn为数列{an}的前n项和,则从2016年到2035年共20年,由等差数列及等比数列的求和公式得:
S20=S10+(a11+a12+1+a20)=477.5+4950×(1-0.9910)≈972.5万…(10分)
(说明:0.9910=(1-0.01)10≈0.9)
∴新政策实施到2035年年人口均值为$\frac{{S}_{20}}{20}$≈48.62 万 …(12分)
由$\frac{{S}_{20}}{20}$<49,故到2035年不需要调整政策. …(12分)
点评 本题考查数列的应用,考查利用数列知识解决实际问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
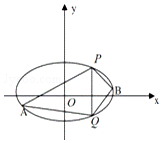 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆C的一个短轴端点与抛物线x2=4y的焦点重合.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33 | B. | 30 | C. | 31 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,$\frac{3}{4}$) | B. | [$\frac{1}{2}$,3) | C. | (-$\frac{3}{2}$,3) | D. | [$\frac{1}{2}$,$\frac{3}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com