
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
【答案】(1)1.
(2) [ -![]() ,0 ).
,0 ).
【解析】分析:第一问首先根据题中所给的函数解析式,将相应的变量代入可得结果,之后应用绝对值不等式的性质得到其差值不超过![]() ,这就得到| m |≤1,解出范围从而求得其最大值,第二问解题的方向就是向最小值靠拢,应用最小值小于零,从而求得参数所满足的条件,求得结果.
,这就得到| m |≤1,解出范围从而求得其最大值,第二问解题的方向就是向最小值靠拢,应用最小值小于零,从而求得参数所满足的条件,求得结果.
详解:(Ⅰ) ∵ f (x) =|x-a|+![]() ,∴f(x+m)=|x+m-a|+
,∴f(x+m)=|x+m-a|+![]() ,
,
∴f(x)-f(x+m)=|x-a|-|x+m-a|≤| m | ,
∴| m |≤1 , ∴-1≤ m ≤1 , ∴ 实数 m 的最大值为 1 ;
( Ⅱ )当 a <![]() 时,g(x)=f(x)+|2x -1|=|x-a|+|2x-1|+
时,g(x)=f(x)+|2x -1|=|x-a|+|2x-1|+![]()
=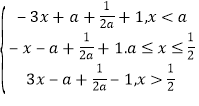
∴ g(x)min =g(![]() )=
)=![]() -a+
-a+![]() =
=![]() ≤0 ,
≤0 ,
∴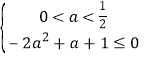 或
或![]() , ∴-
, ∴-![]() ≤a≤0,
≤a≤0,
∴ 实数 a 的取值范围是 [ -![]() ,0 ).
,0 ).


科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第
站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第![]() 站或第
站或第![]() 站时,游戏结束.设棋子位于第
站时,游戏结束.设棋子位于第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋手所走步数之和
次后,求棋手所走步数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,若集合
,若集合![]() 中恰好有3个元素,求实数
中恰好有3个元素,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,其圆心
,其圆心![]() 在抛物线
在抛物线![]() :
:![]() 上,圆
上,圆![]() 过原点且与抛物线
过原点且与抛物线![]() 的准线相切.
的准线相切.
(1)求抛物线![]() 的方程;
的方程;
(2)若过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于直线
且垂直于直线![]() 的直线交抛物线
的直线交抛物线![]() 的准线于点
的准线于点![]() .求
.求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校高三年级学生寒假在家自主学习的情况,随机对该校300名高三学生寒假的每天学习时间(单位:h)进行统计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图所示.
的分组作出频率分布直方图如图所示.

(Ⅰ)根据频率分布直方图计算该校高三年级学生的平均每天学习时间(同一组中的数据用该组区间中点值代表);
(Ⅱ)该校规定学习时间超过4h为合格,否则不合格.已知这300名学生中男生有140人,其中合格的有70人,请补全下表,根据表中数据,能否有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关?
男生 | 女生 | 总计 | |
不合格 | |||
合格 | 70 | ||
总计 | 140 | 160 | 300 |
参考公式: ,其中
,其中![]() .
.
参考附表:
| 0.050 | 0.010 | 0.001 |
3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com