
分析 (1)由过点$(2,\sqrt{2})$且离心率为$\frac{{\sqrt{2}}}{2}$的椭圆C的中心在原点,焦点在x轴上,列出方程组,求出a=2$\sqrt{2}$,b=4,由此能求出椭圆C的方程.
(2)设出直线的方程,将直线的方程与椭圆方程联立,利用二次方程的韦达定理得到弦中点的坐标,根据中点在正方形的内部,得到中点的坐标满足的不等关系,求出k的范围.
解答 解:(1)∵过点$(2,\sqrt{2})$且离心率为$\frac{{\sqrt{2}}}{2}$的椭圆C的中心在原点,焦点在x轴上.
∴设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
则$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}$,解得a=2$\sqrt{2}$,b=4,
∴椭圆C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
(2)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
由题意知直线l的斜率存在,所以设直线l的方程为y=k(x+4)
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0)
由$\left\{\begin{array}{l}{y=k(x+4)}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}$,得(1+2k2)x2+16k2x+32k2-8=0.①
由△=(16k2)2-4(1+2k2)(32k2-8)>0,解得-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$.②
因为x1,x2是方程①的两根,
所以x1+x2=-$\frac{16{k}^{2}}{1+2{k}^{2}}$,于是x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{8{k}^{2}}{1+2{k}^{2}}$,y0=k(x0+4)=$\frac{4k}{1+2{k}^{2}}$.
因为x0=-$\frac{8{k}^{2}}{1+2{k}^{2}}$≤0,所以点G不可能在y轴的右边,
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为$\left\{\begin{array}{l}{{y}_{0}≤{x}_{0}+2}\\{{y}_{0}≥-{x}_{0}-2}\end{array}$,
即$\left\{\begin{array}{l}{\frac{4k}{1+2{k}^{2}}≤-\frac{8{k}^{2}}{1+2{k}^{2}}+2}\\{\frac{4k}{1+2{k}^{2}}≥\frac{8{k}^{2}}{1+2{k}^{2}}-2}\end{array}$,即$\left\{\begin{array}{l}{2{k}^{2}+2k-1≤0}\\{2{k}^{2}-2k-1≤0}\end{array}$,
解得$\frac{-\sqrt{3}-1}{2}$≤k≤$\frac{\sqrt{3}-1}{2}$,
由②得:$\frac{-\sqrt{3}+1}{2}$≤k≤$\frac{\sqrt{3}+1}{2}$.
故直线l斜率的取值范围是[$\frac{-\sqrt{3}+1}{2}$,$\frac{\sqrt{3}+1}{2}$].
点评 求圆锥曲线的方程时,一般利用待定系数法;解决直线与圆锥曲线的位置关系时,一般采用的方法是将直线方程与圆锥曲线方程联立得到关于某个未知数的二次方程,利用韦达定理来找突破口.


科目:高中数学 来源: 题型:填空题
 如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.
如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
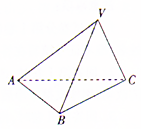 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com