
| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
分析 根据双曲线的渐近线方程,求得b=3a,求得M点坐标,根据三角形的面积公式,及双曲线的性质,即可求得a和b的值,即可求得双曲线方程.
解答 解:由双曲线的焦点在x轴上,双曲线的渐近线方程y=$\frac{b}{a}$x,则b=3a,①
假设M在第一象限,则M(c,$\frac{{b}^{2}}{a}$),
则△MF1F2的面积S=$\frac{1}{2}$×2c×$\frac{{b}^{2}}{a}$=$\frac{{b}^{2}c}{a}$,
即$\frac{{b}^{2}c}{a}$=18$\sqrt{10}$,②
则c2=a2-b2,③
解得:a2=2,b2=18,c2=20,
∴双曲线的标准方程:$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{18}=1$,
故选C.
点评 本题考查双曲线的标准方程及简单几何性质,三角形的面积公式,考查计算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
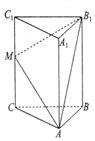 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<2} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
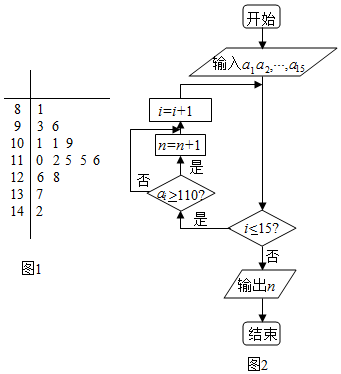 高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )
高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com