
分析 (Ⅰ)由于4Sn=(an+1)2.令n=1,可求得a1,再令n=2,即可求得a2的值,从而可得正项等差数列{an}的公差,继而可求得其通项公式;
(Ⅱ)由(Ⅰ)知an=2n-1,于是可求得其前n项和Sn=n2,故${S}_{n}-\frac{7}{2}{a}_{n}$=${(n-\frac{7}{2})}^{2}-\frac{35}{4}$,从而可求得数列$\{{S_n}-\frac{7}{2}{a_n}\}$的最小值.
解答 (本小题满分13分)
解:(Ⅰ)因为$4{S_n}={({a_n}+1)^2}$,
所以,当n=1时,$4{a_1}={({a_1}+1)^2}$,解得a1=1,
当n=2时,$4(1+{a_2})={({a_2}+1)^2}$,解得a2=-1或a2=3,
因为{an}是各项为正数的等差数列,所以a2=3,
所以{an}的公差d=a2-a1=2,
所以{an}的通项公式an=a1+(n-1)d=2n-1.
(Ⅱ)因为$4{S_n}={({a_n}+1)^2}$,所以${S_n}=\frac{{{{(2n-1+1)}^2}}}{4}={n^2}$,
所以${S_n}-\frac{7}{2}{a_n}={n^2}-\frac{7}{2}(2n-1)$=${n^2}-7n+\frac{7}{2}$=${(n-\frac{7}{2})^2}-\frac{35}{4}$,
所以,当n=3或n=4时,${S_n}-\frac{7}{2}{a_n}$取得最小值$-\frac{17}{2}$.
点评 本题考查数列递推式的应用,考查等差数列的通项公式及二次函数的配方法求最值,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2+i | B. | 2-i | C. | -1+2i | D. | 1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.
如图,四边形ABCD为直角梯形,∠ABC=90°,CB∥DA,AB=20$\sqrt{2}$,DA=10,CB=20,若AB边上有一点P,使得∠CPD最大,则AP=10$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
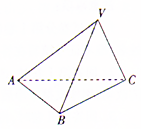 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com