
分析 检验直线方程为x=8,是否符合题意,然后设直线与双曲线相交于A(x1,y1),B(x2,y2),利用点差法求出直线方程后,代入检验所求直线与已知曲线是否相交.
解答 解:当直线的斜率k不存在时,直线方程为x=8,
直线被双曲线所截线段的中点为(8,0),不符合题意;
设直线与双曲线相交于A(x1,y1),B(x2,y2),
把A,B代入到曲线方程可得9x12-16y12=144,9x22-16y22=144,
相减可得,9(x1-x2)(x1+x2)-16(y1-y2)(y1+y2)=0,
由中点坐标公式可得,x1+x2=16,y1+y2=6,
∴kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{9×16}{16×6}$=$\frac{3}{2}$,
直线的方程为y-3=$\frac{3}{2}$(x-8),即为y=$\frac{3}{2}$x-9,
代入双曲线9x2-16y2=144,
可得3x2-48x+160=0,此时△=384>0,满足题意.
故所求直线的方程为3x-2y-18=0.
点评 本题主要考查了点差法在求解直线与曲线相交关系中的应用,学生用“点差法”求出直线方程漏掉检验用“△”验证直线的存在性是导致本题出现错误的最直接的原因.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①② | C. | ③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
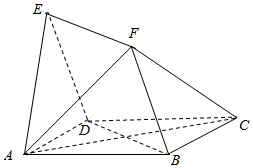 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi |
| 1 | 108 | 82 | 11 | 124 | 80 | 21 | 122 | 64 |
| 2 | 112 | 76 | 12 | 136 | 86 | 22 | 136 | 82 |
| 3 | 130 | 78 | 13 | 127 | 83 | 23 | 114 | 84 |
| 4 | 132 | 91 | 14 | 80 | 73 | 24 | 121 | 80 |
| 5 | 108 | 68 | 15 | 138 | 81 | 25 | 88 | 52 |
| 6 | 140 | 88 | 16 | 141 | 91 | 26 | 142 | 83 |
| 7 | 143 | 92 | 17 | 109 | 85 | 27 | 125 | 69 |
| 8 | 99 | 72 | 18 | 100 | 80 | 28 | 135 | 90 |
| 9 | 106 | 84 | 19 | 92 | 73 | 29 | 112 | 82 |
| 10 | 120 | 77 | 20 | 132 | 82 | 30 | 128 | 92 |
| 数学成绩不优秀 | 数学成绩优秀 | 合计 | |
| 物理成绩不优秀 | |||
| 物理成绩优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}-2$ | C. | $-\frac{{\sqrt{3}}}{2}-2$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
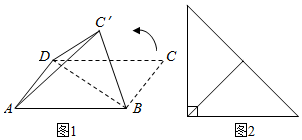
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 两腰长都为$\frac{{\sqrt{3}}}{2}$的等腰三角形 | D. | 两腰长都为$\frac{{\sqrt{2}}}{2}$的等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
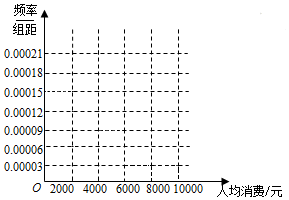 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:| 人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com