
| 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi |
| 1 | 108 | 82 | 11 | 124 | 80 | 21 | 122 | 64 |
| 2 | 112 | 76 | 12 | 136 | 86 | 22 | 136 | 82 |
| 3 | 130 | 78 | 13 | 127 | 83 | 23 | 114 | 84 |
| 4 | 132 | 91 | 14 | 80 | 73 | 24 | 121 | 80 |
| 5 | 108 | 68 | 15 | 138 | 81 | 25 | 88 | 52 |
| 6 | 140 | 88 | 16 | 141 | 91 | 26 | 142 | 83 |
| 7 | 143 | 92 | 17 | 109 | 85 | 27 | 125 | 69 |
| 8 | 99 | 72 | 18 | 100 | 80 | 28 | 135 | 90 |
| 9 | 106 | 84 | 19 | 92 | 73 | 29 | 112 | 82 |
| 10 | 120 | 77 | 20 | 132 | 82 | 30 | 128 | 92 |
| 数学成绩不优秀 | 数学成绩优秀 | 合计 | |
| 物理成绩不优秀 | |||
| 物理成绩优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
分析 (I)根据成绩单对数学成绩和物理成绩进行分类填表,计算K2,对照附表1进行判断;
(II)求出回归系数公式求出回归方程,作出结论.
解答 解:(I)2×2列联表:
| 数学成绩不优秀 | 数学成绩优秀 | 合计 | |
| 物理成绩不优秀 | 6 | 4 | 10 |
| 物理成绩优秀 | 6 | 14 | 20 |
| 合计 | 12 | 18 | 30 |
点评 本题考察查了线性回归方程的解法和独立性检验的统计思想,属于中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
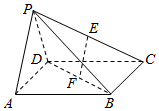 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com