在平行四边形ABCD中.已知AB=3.BC=4.∠ABC=120°.则对角线BD=$\sqrt{13}$,AC=$\sqrt{37}$．题目和参考答案——青夏教育精英家教网—

6．在平行四边形ABCD中，已知AB=3，BC=4，∠ABC=120°，则对角线BD=$\sqrt{13}$；AC=$\sqrt{37}$．

分析直接利用余弦定理求解所求对角线的长度即可．

解答解：平行四边形ABCD中，已知AB=3，BC=4，∠ABC=120°，
则对角线BD=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcos60°}$=$\sqrt{9+16-2×3×4×\frac{1}{2}}$=$\sqrt{13}$．
AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcoa120°}$=$\sqrt{9+16+2×3×4×\frac{1}{2}}$=$\sqrt{37}$．
故答案为：$\sqrt{13}$；$\sqrt{37}$．

点评本题考查余弦定理的应用，考查计算能力．

练习册系列答案

1加1轻巧夺冠小专家课时练练通系列答案

校缘自助课堂系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

19．已知tan$\frac{θ}{2}$=$\frac{1}{2}$，则$\frac{cos（θ-π）sin（π-θ）}{cos（2π-θ）[sin（θ-\frac{π}{2}）+1]}$=-2．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．△ABC中，已知角A，B，C所对的边是a，b，c，则下列说法正确的有②③（写出所有正确命题的编号）．
①若a=2，b=2$\sqrt{3}$，A=30°，则B=60°
②若sinA＞sinB，则a＞b，反之也成立
③若c²sin²B+b²sin²C=2bccosBcosC，则△ABC一定是直角三角形
④若b²=ac且cos（A-C）=$\frac{3}{2}$-cosB，则B=$\frac{π}{3}$或B=$\frac{2π}{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．为了研究数学、物理学习成绩的关联性，某位老师从一次考试中随机抽取30名学生，将数学、物理成绩进行统计，所得数据如表，其中数学成绩在120分以上（含120分）为优秀，物理成绩在80分以上（含80分）为优秀．

编号	数学成绩x_i	物理成绩y_i	编号	数学成绩x_i	物理成绩y_i	编号	数学成绩x_i	物理成绩y_i
1	108	82	11	124	80	21	122	64
2	112	76	12	136	86	22	136	82
3	130	78	13	127	83	23	114	84
4	132	91	14	80	73	24	121	80
5	108	68	15	138	81	25	88	52
6	140	88	16	141	91	26	142	83
7	143	92	17	109	85	27	125	69
8	99	72	18	100	80	28	135	90
9	106	84	19	92	73	29	112	82
10	120	77	20	132	82	30	128	92

（1）根据表格完成下面2×2的列联表：

	数学成绩不优秀	数学成绩优秀	合计
物理成绩不优秀
物理成绩优秀
合计

（2）若这一次考试物理成绩y关于数学成绩x的回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，
由图中数据计算成$\overline{x}$=120，$\overline{y}$=80，$\sum_{i=1}^{n}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）=2736，$\sum_{i=1}^{n}$（x_i-$\overline{x}$）²=8480，若y关于x的回归方程，据此估计，数学成绩每提高10分，物理成绩约提高多少分？（精确到0.1）．
附1：独立性检验：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$

P（K²≥k）	0.15	0.10	0.050	0.010
k	2.072	2.706	3.841	6.635

附2：若（x₁，y₁），（x₂，y₂），…（x_n，y_n）为样本点，$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$为回归直线，
则$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．

如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，BC=5，DC=3，
AD=4，∠PAD=60°．
（1）若M为PA的中点，求证：DM∥平面PBC；
（2）求三棱锥D-PBC的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

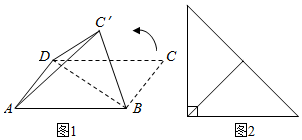
11．如图1，将水平放置且边长为1的正方形ABCD沿对角线BD折叠，使C到C′位置．折叠后三棱锥C′-ABD的俯视图如图2所示，那么其主视图是（　　）

	A．	等边三角形		B．	直角三角形
	C．	两腰长都为$\frac{{\sqrt{3}}}{2}$的等腰三角形		D．	两腰长都为$\frac{{\sqrt{2}}}{2}$的等腰三角形

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．已知直线m，n和平面α，m?α，n∥m，那么“n?α”是“m∥α”的（　　）