
分析 ①若a=2,b=2$\sqrt{3}$,A=30°,由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}}{2}$,由于B∈(0°,180°),即可得出;
②由sinA>sinB,利用正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,即可判断出真假.
③由c2sin2B+b2sin2C=2bccosBcosC,由正弦定理可得:sin2Csin2B+sin2Bsin2C=2sinBsinCcosBcosC,化为:cos(B+C)=0,即可判断出真假;④若b2=ac,利用正弦定理可得:sin2B=sinAsinC.由cos(A-C)=$\frac{3}{2}$-cosB=$\frac{3}{2}$+cos(A+C),化为:sinAsinC=$\frac{3}{4}$,即可判断出真假.
解答 解:①若a=2,b=2$\sqrt{3}$,A=30°,由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,可得sinB=$\frac{bsinA}{a}$=$\frac{2\sqrt{3}sin3{0}^{°}}{2}$=$\frac{\sqrt{3}}{2}$,B∈(0°,180°),b>a,
则B=60°或120°,因此不正确.
②若sinA>sinB,由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,∴a>b,反之也成立,正确.
③若c2sin2B+b2sin2C=2bccosBcosC,由正弦定理可得:sin2Csin2B+sin2Bsin2C=2sinBsinCcosBcosC,化为:sinBsinC=cosBcosC,
∴cos(B+C)=0,∵0<B+C<π,∴B+C=$\frac{π}{2}$,则△ABC一定是直角三角形,正确.
④若b2=ac,则sin2B=sinAsinC.由cos(A-C)=$\frac{3}{2}$-cosB=$\frac{3}{2}$+cos(A+C),化为:sinAsinC=$\frac{3}{4}$.∴sinB=$\frac{\sqrt{3}}{2}$,又B∈(0,π),则B=$\frac{π}{3}$或B=$\frac{2π}{3}$,由b2=ac,可知:B不是最大角,因此是锐角,∴B=$\frac{π}{3}$,因此不正确.
综上可得:正确的为②③.
故答案为:②③.
点评 本题考查了正弦定理的应用、三角形内角和定理、和差公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
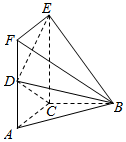 如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.
如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
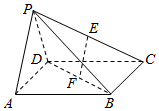 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com