
分析 由数列递推式求出首项,写出n≥2时的递推式,作差后对n分偶数和奇数讨论,求出数列通项公式,可得函数an=$\frac{1}{{2}^{n+1}}$-1(n为正奇数)为减函数,最大值为a1=-$\frac{3}{4}$,函数an=3-$\frac{1}{{2}^{n}}$(n为正偶数)为增函数,最小值为a2=$\frac{11}{4}$,再由(t-an+1)(t-an)<0恒成立求得实数t的取值范围.
解答 解:由Sn=(-1)nan+$\frac{1}{{2}^{n}}$+n-3,得a1=-$\frac{3}{4}$;
当n≥2时,an=Sn-Sn-1=(-1)nan+$\frac{1}{{2}^{n}}$+n-3-(-1)n-1an-1-$\frac{1}{{2}^{n-1}}$-(n-1)+3
=(-1)nan+(-1)nan-1-$\frac{1}{{2}^{n}}$+1,
若n为偶数,则an-1=$\frac{1}{{2}^{n}}$-1,∴an=$\frac{1}{{2}^{n+1}}$-1(n为正奇数);
若n为奇数,则an-1=-2an-$\frac{1}{{2}^{n}}$+1=2($\frac{1}{{2}^{n+1}}$-1)-$\frac{1}{{2}^{n}}$+1=3-$\frac{1}{{2}^{n-1}}$,
∴an=3-$\frac{1}{{2}^{n}}$(n为正偶数).
函数an=$\frac{1}{{2}^{n+1}}$-1(n为正奇数)为减函数,最大值为a1=-$\frac{3}{4}$,
函数an=3-$\frac{1}{{2}^{n}}$(n为正偶数)为增函数,最小值为a2=$\frac{11}{4}$,
若(t-an+1)(t-an)<0恒成立,
则a1<t<a2,即-$\frac{3}{4}$<t<$\frac{11}{4}$.
故答案为:(-$\frac{3}{4}$,$\frac{11}{4}$).
点评 本题考查数列递推式,考查了数列通项公式的求法,体现了分类讨论的数学思想方法和数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi | 编号 | 数学成绩xi | 物理成绩yi |
| 1 | 108 | 82 | 11 | 124 | 80 | 21 | 122 | 64 |
| 2 | 112 | 76 | 12 | 136 | 86 | 22 | 136 | 82 |
| 3 | 130 | 78 | 13 | 127 | 83 | 23 | 114 | 84 |
| 4 | 132 | 91 | 14 | 80 | 73 | 24 | 121 | 80 |
| 5 | 108 | 68 | 15 | 138 | 81 | 25 | 88 | 52 |
| 6 | 140 | 88 | 16 | 141 | 91 | 26 | 142 | 83 |
| 7 | 143 | 92 | 17 | 109 | 85 | 27 | 125 | 69 |
| 8 | 99 | 72 | 18 | 100 | 80 | 28 | 135 | 90 |
| 9 | 106 | 84 | 19 | 92 | 73 | 29 | 112 | 82 |
| 10 | 120 | 77 | 20 | 132 | 82 | 30 | 128 | 92 |
| 数学成绩不优秀 | 数学成绩优秀 | 合计 | |
| 物理成绩不优秀 | |||
| 物理成绩优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
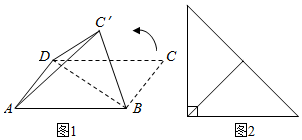
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 两腰长都为$\frac{{\sqrt{3}}}{2}$的等腰三角形 | D. | 两腰长都为$\frac{{\sqrt{2}}}{2}$的等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
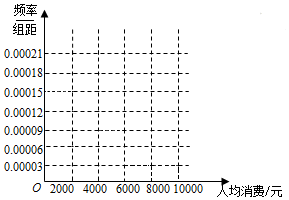 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:| 人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q真 | B. | p∨q真 | C. | (¬p)∧q为假 | D. | (¬p)∧(¬q)为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {x|0<x≤1} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com