Question

12．设△ABC的三个内角A，B，C所对的边分别为a，b，c，点O为△ABC的外接圆的圆心，若满足a+b≥2c．
（1）求角C的最大值；
（2）当角C取最大值时，己知a=b=$\sqrt{3}$，点P为△ABC外接圆圆弧上-点，若$\overline{OP}=x\overline{OA}+y\overline{OB}$，求x•y的最大值．

Answer 1

分析 （1）由余弦定理可以得到$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$，而由a+b≥2c即可得出-c²的范围，从而得出a²+b²-c²的范围，进一步便可得到$cosC≥\frac{1}{2}$，从而有$0＜C≤\frac{π}{3}$，这便说明角C的最大值为$\frac{π}{3}$；
（2）$C=\frac{π}{3}$时便可得出△ABC为等边三角形，从而可求得外接圆半径为1，并可求得$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{1}{2}$，从而对$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$两边平方便可得到x²+y²=xy+1≥2xy，这样便可得出xy的最大值．

解答 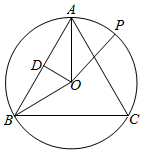解：（1）在△ABC中由余弦定理得，$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$；
∵a+b≥2c；
∴$-{c}^{2}≥-（\frac{a+b}{2}）^{2}=-\frac{{a}^{2}}{4}-\frac{{b}^{2}}{4}-\frac{ab}{2}$；
∴${a}^{2}+{b}^{2}-{c}^{2}≥\frac{3}{4}{a}^{2}+\frac{3}{4}{b}^{2}-\frac{ab}{2}$；
∴$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}≥\frac{3}{8}（\frac{a}{b}+\frac{b}{a}）-\frac{1}{4}$；
∵$\frac{a}{b}+\frac{b}{a}≥2$，当且仅当a=b时取“=”；
∴$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}≥\frac{1}{2}$；
即$cosC≥\frac{1}{2}$；
∴$0＜C≤\frac{π}{3}$；
∴角C的最大值为$\frac{π}{3}$；
（2）当角C取最大值$\frac{π}{3}$时，∵$a=b=\sqrt{3}$；
∴△ABC为等边三角形；
∴O为△ABC的中心，如图所示，D为边AB的中点，连接OD，则：
OD⊥AB，且$∠DAO=30°，AD=\frac{\sqrt{3}}{2}$；
∴OA=1，即外接圆半径为1，且∠AOB=120°；
∴$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{1}{2}$；
∴对$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$两边平方得，${\overrightarrow{OP}}^{2}={x}^{2}{\overrightarrow{OA}}^{2}+{y}^{2}{\overrightarrow{OB}}^{2}+2xy\overrightarrow{OA}•\overrightarrow{OB}$；
∴1=x²+y²-xy；
∴x²+y²=xy+1≥2xy，当且仅当x=y时取“=”；
∴xy≤1；
∴x•y的最大值为1．

点评 考查余弦定理，不等式的性质，基本不等式及不等式a²+b²≥2ab的运用，以及向量数量积的运算及计算公式，清楚三角形外接圆的概念．