
分析 点(1,1)到直线xcosα+ysinα=2的距离为d.可得d=|cosα+sinα-2|.
(1)d=$\frac{2}{3}$,则$\frac{2}{3}$=|cosα+sinα-2|,可得cosα+sinα=2-$\frac{2}{3}$,两边平方化简即可得出.
(2)d=|cosα+sinα-2|=$|\sqrt{2}sin(α+\frac{π}{4})-2|$,即可得出.
解答 解:点(1,1)到直线xcosα+ysinα=2的距离为d.
∴d=$\frac{|cosα+sinα-2|}{\sqrt{co{s}^{2}α+si{n}^{2}α}}$=|cosα+sinα-2|.
(1)d=$\frac{2}{3}$,则$\frac{2}{3}$=|cosα+sinα-2|,
∴cosα+sinα=2$±\frac{2}{3}$,
∵cosα+sinα=$\sqrt{2}sin(α+\frac{π}{4})$$≤\sqrt{2}$,∴cosα+sinα≠2+$\frac{2}{3}$,
∴cosα+sinα=2-$\frac{2}{3}$=$\frac{4}{3}$,
两边平方可得:1+2sinαcosα=$\frac{16}{9}$,化为:sin2α=$\frac{7}{9}$.
(2)d=|cosα+sinα-2|=$|\sqrt{2}sin(α+\frac{π}{4})-2|$≤$\sqrt{2}$+2.当且仅当$sin(α+\frac{π}{4})$=-1时取等号.
∴d的最大值为$\sqrt{2}$+2.
点评 本题考查了三角函数求值、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
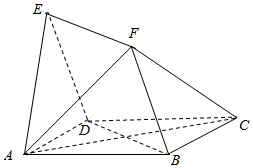 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com