
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
分析 根据求出首项和公差,得到数列的通项公式,再判断数列的前7项为正数,再根据裂项求和即可得到答案.
解答 解:∵Sm-1=13,Sm=0,Sm+1=-15,
∴am=Sm-Sm-1=0-13=-13,am+1=Sm+1-Sm=-15-0=-15,
又∵数列{an}为等差数列,
∴公差d=am+1-am=-15-(-13)=-2,
∴$\left\{\begin{array}{l}{(m{-1)a}_{1}+\frac{(m-1)(m-2)}{2}×(-2)=13}\\{m{a}_{1}+\frac{m(m-1)}{2}×(-2)=0}\end{array}\right.$,
解得a1=13
∴an=a1+(n-1)d=13-2(n-1)=15-2n,
当an≥0时,即n≤7.5,
当an+1≤0时,即n≥6.5,
∴数列的前7项为正数,
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(15-2n)(13-2n)}$=$\frac{1}{2}$($\frac{1}{13-2n}$-$\frac{1}{15-2n}$)
∴数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为$\frac{1}{2}$($\frac{1}{11}$-$\frac{1}{13}$+$\frac{1}{9}$-$\frac{1}{11}$+$\frac{1}{7}$-$\frac{1}{9}$+…+1-$\frac{1}{3}$)=$\frac{1}{2}$(1-$\frac{1}{13}$)=$\frac{6}{13}$.
故选:D
点评 本题考查了等差数列的性质和等差数列的前n项和,以及数列的函数的特征和裂项求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象关于原点对称 | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | |
| C. | 函数f(x)图象上的所有点向右平移$\frac{π}{3}$个单位长度后,所得的图象关于原点对称 | |
| D. | 函数f(x)在区间(0,π)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
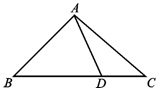 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数且它的图象关于点(π,0)对称 | |
| B. | 偶函数且它的图象关于点$(\frac{3π}{2},0)$对称 | |
| C. | 奇函数且它的图象关于点(π,0)对称 | |
| D. | 奇函数且它的图象关于点$(\frac{3π}{2},0)$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com