
分析 构造函数f(x)=xsinx,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],判断函数f(x)为偶函数,利用f′(x)判断f(x)=xsinx在x∈[0,$\frac{π}{2}$]上的单调性,从而选出正确答案.
解答 解:根据题意,令f(x)=xsinx,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
∵f(-x)=-x•sin(-x)=x•sinx=f(x),
∴f(x)=xsinx,在x∈[-$\frac{π}{2}$,$\frac{π}{2}$]上为偶函数;
又f′(x)=sinx+xcosx,
∴当x∈[0,$\frac{π}{2}$],f′(x)>0,
∴f(x)=xsinx在x∈[0,$\frac{π}{2}$]单调递增;
同理可证偶函数f(x)=xsinx在x∈[-$\frac{π}{2}$,0]单调递减;
∴当0≤|β|<|α|≤$\frac{π}{2}$时,f(α)>f(β),即αsinα-βsinβ>0,反之也成立,
∴α2>β2,④正确;
其他命题不一定成立.
故答案为:④.
点评 本题考查了正弦函数的单调性,解题时应构造函数f(x)=xsinx,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],研究函数f(x)=xsinx的奇偶性与单调性解决问题,是难题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
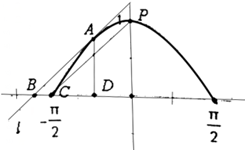 直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.
直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com