练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．若（3x-$\sqrt{7}$）4=a0+a1x+a2x2+a3x3+a4x4，则（a0+a2+a4）2-（a1+a3）2=16．

    分析 在（3x-$\sqrt{7}$）4=a0+a1x+a2x2+a3x3+a4x4中利用赋值法，分别令x=1可求a0+a1+a2+a3+a4，令x=-1可求a0-a1+a2-a3+a4），而（a0+a2+a4）2-（a1+a3）2=（a0+a1+a2+a3+a4）（a0-a1+a2-a3+a4），代入可求．

    解答 解：在（3x-$\sqrt{7}$）4=a0+a1x+a2x2+a3x3+a4x4中
    令x=1可得，a0+a1+a2+a3+a4=（3-$\sqrt{7}$）4，
    令x=-1可得，a0-a1+a2-a3+a4=（-3-$\sqrt{7}$）4，
    ∴（a0+a2+a4）2-（a1+a3）2=（a0+a1+a2+a3+a4）（a0-a1+a2-a3+a4）=（3-$\sqrt{7}$）4（-3-$\sqrt{7}$）4=16，
    故答案为：16．

    点评 本题主要考查了二项展开式中利用赋值法求解二项展开式的各项系数之和（注意是各项系数之和，要区别于二项式系数之和），解答本题还要注意所求式子的特点：符合平方差公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．如图是一个四棱锥的三视图，则该几何体的体积为（　　）
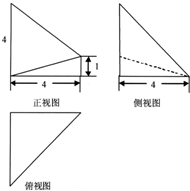
    A．$\frac{40}{3}$B．$\frac{32}{3}$C．$\frac{16}{3}$D．$\frac{28}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．在△ABC中，已知a=$\frac{4\sqrt{3}}{3}$，b=4，A=30°，则△ABC的面积为$\frac{8}{3}\sqrt{3}$或$\frac{4}{3}\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若幂函数f（x）=xa的图象经过点（3，$\sqrt{3}$），则f（4）的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知复数z1=1+2i，z2=2-2i，i为虚数单位．
    （1）若复数az1+z2在复平面内对应的点在第三象限，求实数a的取值范围；
    （2）若z=$\frac{{z}_{1}+{z}_{2}}{{z}_{1}-{z}_{2}}$，求z的共轭复数$\overline{z}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若复数$z=\frac{1+i}{1-i}，则{z^{2010}}$=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（1）已知tanα=2，求$\frac{sinα+cosα}{sinα-cosα}$的值；
    （2）已知$sinα=-\frac{3}{5}$，且α第三象限角，求 $\frac{{sin（2π-α）cos（π+α）cos（\frac{π}{2}+α）cos（\frac{11π}{2}-α）}}{{cos（π-α）sin（3π-α）sin（-π-α）sin（\frac{9π}{2}+α）}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知A（1，2），B（2，3），C（-2，5）为平面直角坐标系xOy内三点，其中O为坐标原点．
    （Ⅰ）求证：$\overrightarrow{AB}⊥\overrightarrow{AC}$；
    （Ⅱ）若D为x轴上一点，且$\overrightarrow{AD}$与$\overrightarrow{BC}$共线，求D点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．直线y=kx+b与曲线y=x3-3x+1相切于点（2，3），则b的值为（　　）
    A．-3B．9C．-7D．-15

    查看答案和解析>>

    同步练习册答案