练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知全集∪=A∪B∪C，又知card（∪）=24，card（A）=12，card（B）=10，card（C）=13，card（A∩B∩C）=2，则card（（A∩B）∪（B∩C）∪（C∩A））=9．

    分析 作出韦恩图，根据元素个数列出方程解出．

    解答 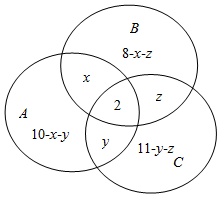解：作出韦恩图如图所示：则全集U中的元素分为7部分，
    设card（A∩B∩∁UC）=x，card（A∩C∩∁UB）=y，card（B∩C∩∁UA）=z，
    则card（∁U（B∪C））=10-x-y，card（∁U（A∪C））=8-x-z，card（∁U（A∪B））=11-y-z．
    ∵card（∪）=24，∴（10-x-y）+x+y+2+（8-x-z）+z+（11-y-z）=24，
    ∴x+y+z=7．
    ∴card（（A∩B）∪（B∩C）∪（C∩A））=x+y+z+2=9．
    故答案为：9．

    点评 本题考查了元素个数的计算，使用韦恩图可使计算直观，简单．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．关于下列命题：
    ①函数f（x）=|2cos2x-1|最小正周期是π；
    ②函数y=cos2（$\frac{π}{4}$-x）是偶函数；
    ③函数y=4sin（2x-$\frac{π}{3}$）的一个对称中心是（$\frac{π}{6}$，0）；
    ④关于x的方程sinx+$\sqrt{3}$cosx=a（0≤x≤$\frac{π}{2}$）有两相异实根，则实数a的取值范围是（1，2）．
    写出所有正确的命题的题号：③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若（x+$\frac{2}{x}$）n的展开式中各项的系数之和为81，且常数项为a，则直线y=$\frac{a}{6}$x与曲线y=x2所围成的封闭区域面积为$\frac{32}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

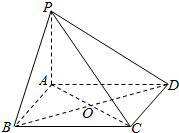    2．如图所示，PA垂直于正方形ABCD所在的平面，A为垂足，点O为正方形ABCD对角线AC和BD的交点．
    （1）判断CD与平面PAD是否垂直？
    （2）判断平面PCD与平面PAD是否垂直？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若A，B是半径为1的球面上的两个点，过这两个点的半径夹角为90°，则A，B两点的球面距离为$\frac{π}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=2$\sqrt{3}$cos2x+2sinxcosx-m的最大值为2，求函数的最小正周期和m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=ax2-2x+2，若f（x）在区间（1，4）上有f（x）＞0恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知$\overrightarrow{a}$=（3，-1），$\overrightarrow{b}$=（1，-2），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若命题p是假命题，命题q是真命题，则（　　）
    A．p∧q是真命题B．p∨q是假命题C．?p是假命题D．￢q是假命题

    查看答案和解析>>

    同步练习册答案