
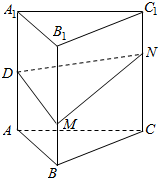
 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |
分析 由BM=C1N,得线段MN必过正方形BCC1B1的中心O,由DO⊥平面BCC1B1,可得平面DMN⊥平面BCC1B1;
由△A1DM的面积不变,N到平面A1DM的距离不变,得到三棱锥A1-DMN的体积为定值;
利用反证法思想说明△DMN不可能为直角三角形;
平面DMN与平面ABC平行时所成角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大.
解答 解:如图,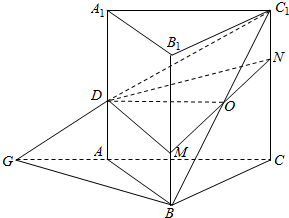
当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,而DO⊥平面BCC1B1,∴平面DMN⊥平面BCC1B1,A正确;
当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,∴棱锥N-A1DM的体积不变,即三棱锥A1-DMN的体积为定值,B正确;
若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,∴△DMN不可能为直角三角形,C错误;
当M、N分别为BB1,CC1中点时,平面DMN与平面ABC所成的角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大,为∠C1BC,等于$\frac{π}{4}$.
∴平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$],D正确.
故选:C.
点评 本题考查了命题的真假判断与应用,考查了棱柱的结构特征,考查了空间想象能力和思维能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 560 | B. | 880 | C. | 1120 | D. | 1440 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=0是常值函数中唯一一个“t型函数” | |
| B. | f(x)=x2是一个“t型函数” | |
| C. | f(x)=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D. | “$\frac{1}{2}$型函数”至少有一个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com