
分析 将所求展开,利用已知三个向量为单位向量,并且$\overrightarrow{a}•\overrightarrow{b}$=0,得到所求为$\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})$+1,利用商量下公式求最值.
解答 解:由已知得到$(\overrightarrow{a}+\overrightarrow{c})•(\overrightarrow{b}+\overrightarrow{c})$=$\overrightarrow{a}•\overrightarrow{b}+\overrightarrow{a}•\overrightarrow{c}+\overrightarrow{c}•\overrightarrow{b}+{\overrightarrow{c}}^{2}$=$\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})$+1;
根据几何意义,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$,设$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$的夹角为θ,则$\overrightarrow{c}•(\overrightarrow{a}+\overrightarrow{b})$+1=($\sqrt{2}+1$)cosθ,所以最大值为$\sqrt{2}+1$;
故答案为:$1+\sqrt{2}$.
点评 本题考查了向量的数量积公式的运用;关键是将所求变形为向量夹角的式子.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
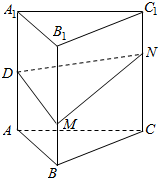 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:
如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com