
分析 (I)f(x)=$\left\{\begin{array}{l}{-\frac{3}{2}x-1,x<-2}\\{-\frac{1}{2}x+1,-2≤x≤0}\\{\frac{3}{2}x+1,x>0}\end{array}\right.$,利用一次函数的单调性即可得出a.
(II)由(I)可知:m2+n2=1,利用基本不等式的性质可得:1≥2mn,由于m,n>0,再利用基本不等式的性质即可得出$\frac{1}{m}$+$\frac{1}{n}$的最小值.
解答 解:(I)f(x)=$\left\{\begin{array}{l}{-\frac{3}{2}x-1,x<-2}\\{-\frac{1}{2}x+1,-2≤x≤0}\\{\frac{3}{2}x+1,x>0}\end{array}\right.$,
∴当x<-2时,f(x)>f(-2)=2;
当-2≤x≤0时,f(x)>f(0)=1;
当x>0时,f(x)>f(0)=1.
综上可得:函数f(x)的最小值为1,∴a=1.
(II)由(I)可知:m2+n2=1,
∴1≥2mn,∴$mn≤\frac{1}{2}$.
∵m,n>0,∴$\frac{1}{m}$+$\frac{1}{n}$≥2$\sqrt{\frac{1}{mn}}$≥2$\sqrt{2}$,当且仅当m=n=$\frac{\sqrt{2}}{2}$时取等号.
∴$\frac{1}{m}$+$\frac{1}{n}$的最小值为2$\sqrt{2}$.
点评 本题考查了分段函数与一次函数的性质、基本不等式的性质,考查了数形结合的思想方法与推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{2a}$ | B. | y=-$\frac{1}{4a}$ | C. | y=$\frac{1}{2a}$ | D. | y=$\frac{1}{4a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1或一1 | C. | 2 | D. | 2或一2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:AD•DE=2PB2.
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:AD•DE=2PB2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,lnx≥x | B. | ?x>0,lnx≥x | C. | ?x≤0,lnx<x | D. | ?x>0,lnx<x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | -$\frac{4}{9}$ | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
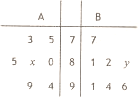 某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.
某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com