
分析 ①设C(cosθ,sinθ)(θ∈(cosθ,sinθ),θ∈[0,2π).可得$\overrightarrow{OA}$•$\overrightarrow{OC}$=acosθ(a>1),可得最小值,即可判断出正误;
②不妨取B(1,0),则△OBC面积=$\frac{1}{2}×1×sinθ$$≤\frac{1}{2}$,即可判断出正误;
③若a=$\sqrt{2}$,且直线AB,AC都与圆O相切,则∠BAO=∠CAO=45°,即可判断出△ABC的形状,即可判断出正误;
④若a=$\sqrt{2}$,且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$(λ>0),可知:A,B,C三点共线,设AB:my=x-$\sqrt{2}$(m<0),联立与圆的方程联立化为$(1+{m}^{2}){y}^{2}+2\sqrt{2}my$+1=0,△>0,利用根与系数的关系可得|BC|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,原点O直线AC的距离d=$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$,可得S△OBC=$\frac{1}{2}|BC|d$,再利用基本不等式的性质即可得出,即可判断出正误;
⑤若a=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$,设B(x1,y1),C(x2,y2),D(x0,y0),直线AB的方程为:y=$k(x-\frac{\sqrt{5}}{2})$,与圆的方程联立化为(4+4k2)x2-$4\sqrt{5}{k}^{2}$x+5k2-4=0,△>0.利用圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$,可得x0=x1+x2,y0=y1+y2,代入圆的方程化简即可解出,即可判断出正误.
解答 解:①设C(cosθ,sinθ)(θ∈(cosθ,sinθ),θ∈[0,2π).∴$\overrightarrow{OA}$•$\overrightarrow{OC}$=acosθ(a>1),因此最小值为-a,故不正确;
②不妨取B(1,0),则△OBC面积=$\frac{1}{2}×1×sinθ$$≤\frac{1}{2}$,其最大值为$\frac{1}{2}$,因此不正确;
③若a=$\sqrt{2}$,且直线AB,AC都与圆O相切,则∠BAO=∠CAO=45°,则△ABC为等腰直角三角形,因此不正确;
④若a=$\sqrt{2}$,且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$(λ>0),可知:A,B,C三点共线,设AB:my=x-$\sqrt{2}$(m<0),联立$\left\{\begin{array}{l}{my=x-\sqrt{2}}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,化为$(1+{m}^{2}){y}^{2}+2\sqrt{2}my$+1=0,△>0,|m|>1.∴y1+y2=$\frac{-2\sqrt{2}m}{1+{m}^{2}}$,y1y2=$\frac{1}{1+{m}^{2}}$,
∴|BC|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$2\sqrt{\frac{{m}^{2}-1}{{m}^{2}+1}}$,原点O直线AC的距离d=$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$,∴S△OBC=$\frac{1}{2}|BC|d$=$\frac{1}{2}×$$2\sqrt{\frac{{m}^{2}-1}{{m}^{2}+1}}$×$\frac{\sqrt{2}}{\sqrt{1+{m}^{2}}}$=$\sqrt{2}$×$\sqrt{\frac{{m}^{2}-1}{(1+{m}^{2})^{2}}}$=$\sqrt{2}$$\sqrt{\frac{1}{{m}^{2}-1+\frac{4}{{m}^{2}-1}+4}}$≤$\sqrt{2}×\sqrt{\frac{1}{4+4}}$=$\frac{1}{2}$,当且仅当m2=3时取等号,即△OBC面积取得最大值$\frac{1}{2}$,此时|AB|=2×$\sqrt{\frac{3-1}{3+1}}$=1,因此不正确;
⑤若a=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$,设B(x1,y1),C(x2,y2),D(x0,y0),直线AB的方程为:y=$k(x-\frac{\sqrt{5}}{2})$,
联立$\left\{\begin{array}{l}{y=k(x-\frac{\sqrt{5}}{2})}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,化为(4+4k2)x2-$4\sqrt{5}{k}^{2}$x+5k2-4=0,△>0,∴x1+x2=$\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}}$,y1+y2=k(x1+x2)-$\sqrt{5}$k
=$-\frac{4\sqrt{5}k}{4+4{k}^{2}}$,∵圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$,∴x0=x1+x2=$\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}}$,y0=y1+y2=$-\frac{4\sqrt{5}k}{4+4{k}^{2}}$,∴$(\frac{4\sqrt{5}{k}^{2}}{4+4{k}^{2}})^{2}$+$(-\frac{4\sqrt{5}k}{4+4{k}^{2}})^{2}$=1,化为4k4+3k2-1=0,解得$k=±\frac{1}{2}$,∴直线BC的斜率是$±\frac{1}{2}$,正确.
综上可得:只有⑤正确.
故答案为:⑤.
点评 本题综合考查了直线与圆的相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、向量数量积运算性质、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 乙队胜的概率 | 乙队平的概率 | 乙队负的概率 | |
| 与丙 队比赛 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 与丁队比赛 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M∪N=R | C. | N?M | D. | M?N |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
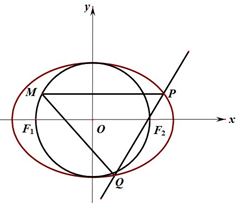 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com