
分析 (1)①根据排列数公式证明即可,②由①得C2n+2n+1=C2n+1n+C2n+1n+1=2C${\;}_{2n+1}^{n}$;
(2)①甲获胜的概率P=p3(6p2-15p+10),
②设乙每一局获胜的概率为q,则p+q=1,0<q<$\frac{1}{2}$.记在甲最终获胜的概率为Pn,根据超几何分布得到Pn,利用(1)的结论计算Pn-Pn+1<0,问题得以证明.
解答 解:(1)①Cnr+Cnr+1=$\frac{n!}{r!(n-r)!}$+$\frac{n!}{(r+1)!(n-r-1)!}$=$\frac{n![(r+1)+(n-r)]}{(r+1)!(n-r)!}$=$\frac{(n+1)!}{(r+1)![(n+1)-(r+1)]!}$=Cn+1r+1;
②由①得C2n+2n+1=C2n+1n+C2n+1n+1=2C${\;}_{2n+1}^{n}$;
(2)①若n=2,甲获胜的概率P=p3+pC32p2(1-p)+pC42p2(1-p)2=p3(6p2-15p+10),
②证明:设乙每一局获胜的概率为q,则p+q=1,0<q<$\frac{1}{2}$.
记在甲最终获胜的概率为Pn,则Pn=pn+1+pCn+1npnq+pCn+2npnp2+…+pC2nnpnqn=pn+1(1+Cn+1nq+Cn+2nq2+…+C2nnqn),
∴Pn-Pn+1=pn+1(1+Cn+1nq+Cn+2nq2+…+C2nnqn)-pn+2(1+Cn+2n+1q+Cn+3n+1q2+…+C2n+2n+1qn+1),
=pn+1[(1+Cn+1nq+Cn+2nq2+…+C2nnqn)-(1-q)(1+Cn+2n+1q+Cn+3n+1q2+…+C2n+2n+1qn+1)],
=pn+1[(1+Cn+1nq+Cn+2nq2+…+C2nnqn)-(1+Cn+2n+1q+Cn+3n+1q2+…+C2n+2n+1qn+1)+q(1+Cn+2n+1q+Cn+3n+1q2+…+C2n+2n+1qn+1)],
=pn+1[(1-1)+q(Cn+1n-Cn+2n+1+1)+q2(Cn+2n-Cn+3n+1+1)+…+qn(C2nn-C2n+1n+1+C2nn+1)-qn+1)(C2n+2n+1-C2n+1n+1+qn+2C2n+2n+1],
=pn+1[-qn+1)(C2n+2n+1-C2n+1n+1+qn+2C2n+2n+1],
=pn+1qn+1(qC2n+2n+1-C2n+1n+1)],
=pn+1qn+1(2qC2n+1n-C2n+1n)],
=pn+1qn+1C2n+1n(2q-1)<0,
所以Pn<Pn+1,
即总局数越多,甲获胜的可能性越大(即甲获胜的概率越大).
点评 本题考查了排列数公式的应用,本题的运算量很大,需要耐心和认真,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 乙队胜的概率 | 乙队平的概率 | 乙队负的概率 | |
| 与丙 队比赛 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 与丁队比赛 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,lnx≥x | B. | ?x>0,lnx≥x | C. | ?x≤0,lnx<x | D. | ?x>0,lnx<x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
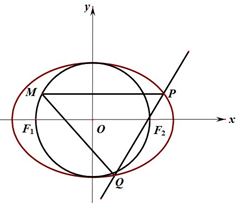 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (11+$4\sqrt{2}$)π | B. | (12+4$\sqrt{2}$)π | C. | (13+4$\sqrt{2}$)π | D. | (14+4$\sqrt{2}$)π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com