
| A. | f(x)=0是常值函数中唯一一个“t型函数” | |
| B. | f(x)=x2是一个“t型函数” | |
| C. | f(x)=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D. | “$\frac{1}{2}$型函数”至少有一个零点 |
分析 举例说明A不正确;把f(x)=x2代入定义求得λ的矛盾的值说明B错误;把f(x)=|x-$\frac{1}{2}$|代入定义求得λ的矛盾的值说明C错误;由函数零点存在性定理结合新定义说明D正确.
解答 解:由题意得,A不正确,如f(x)=c≠0,取t=-1,则f(x-1)-f(x)=c-c=0,
即f(x)=c≠0是一个“t函数”;
若f(x)=x2是一个“关于t函数”,则(x+λ)2+λx2=0,求得λ=0且λ=-1,矛盾.B不正确;
若f(x)=|x-$\frac{1}{2}$|是一个“关于t函数”,则|x+λ-$\frac{1}{2}$|+λ|x-$\frac{1}{2}$|=0,求得λ=0且λ=-$\frac{1}{2}$,矛盾,C不正确;
D正确,若f(x)是“是关于$\frac{1}{2}$函数”,则f(x+$\frac{1}{2}$)+$\frac{1}{2}$f(x)=0,取x=0,则f($\frac{1}{2}$)+$\frac{1}{2}$f(0)=0,
若f(0)、f ($\frac{1}{2}$)任意一个为0,则函数f(x)有零点;若f(0)、f ($\frac{1}{2}$)均不为0,
则f(0)、f ($\frac{1}{2}$)异号,由零点存在性定理知,在(0,$\frac{1}{2}$)区间内存在零点;
故选:D.
点评 本题是新定义题,考查了函数的性质,关键是对题意的理解,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
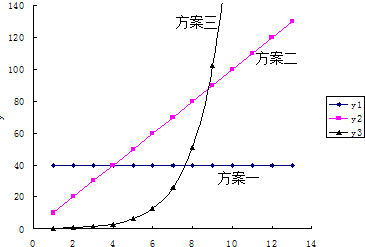
| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
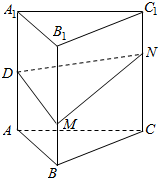 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:
如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com