
分析 运用条件定义在R上的奇函数f(x)满足f(x+4)=-f(x),得出函数f(x)周期为8,x=2,x=-2均为对称轴,即可判断每一个选项正确与否.
解答 解:由条件可知,函数f(x)周期为8,x=2,x=-2均为对称轴,
①中,令x=-1,则f(3)=f(4-1)=-f(-1)=f(1)=log2(1+1)=1,故①正确;
②中,f(x)在[-2,2]上单调递增,由f(x)关于x=-2对称,所以f(x)在在[-6,-2]上是减函数;
故②正确;
③中,f(0)≠f(2),可知f(x)的图象不关于直线x=1对称;故③不正确;
④中,函数f(x)的图象关于直线x=-6,x=2对称;,可知f(x)=m,(m∈(0,1))的根有4个,分别记为x1,x2,x3,x4,
有$\frac{{x}_{1}+{x}_{2}}{2}$=-6,$\frac{{x}_{3}+{x}_{4}}{2}$=2,故x1+x2+x3+x4=8
故④正确
故答案为:①②④
点评 本题考查了函数的性质,函数的周期性,对称性,单调性的综合运用,属于中档题,考查了学生的分析问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=0是常值函数中唯一一个“t型函数” | |
| B. | f(x)=x2是一个“t型函数” | |
| C. | f(x)=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D. | “$\frac{1}{2}$型函数”至少有一个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 乙队胜的概率 | 乙队平的概率 | 乙队负的概率 | |
| 与丙 队比赛 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 与丁队比赛 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
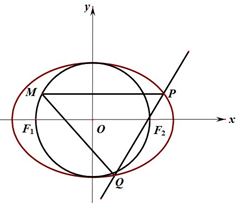 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com