
分析 (Ⅰ)求出导数,由题意可得f′(0)=1+b=0,即可得到b的值;
(Ⅱ)求出f(x)的解析式,构造函数$g(x)={(x+1)^2}ln(x+1)-x-\frac{3}{2}{x^2}$,(x≥0),求出导数,判断符号,确定函数的单调性,即可得证;
(Ⅲ)设h(x)=(x+1)2ln(x+1)-x-mx2,讨论①当$m≤\frac{3}{2}$时,②当$m>\frac{3}{2}$时,通过导数判断单调性,即可得到所求范围.
解答 解:(Ⅰ) 定义域为(-1,+∞),f′(x)=2(x+1)ln(x+1)+(x+1)+b,
f′(0)=1+b=0,解得b=-1;
(Ⅱ)证明:f(x)=(x+1)2ln(x+1)-x,
设$g(x)={(x+1)^2}ln(x+1)-x-\frac{3}{2}{x^2}$,(x≥0),
g′(x)=2(x+1)ln(x+1)-2x,(g′(x))′=2ln(x+1)≥0,
∴g′(x)在[0,+∞)上单调递增,∴g′(x)≥g′(0)=0,
∴g(x)在[0,+∞)上单调递增,∴g(x)≥g(0)=0.
∴$f(x)≥\frac{3}{2}{x^2}$.
(Ⅲ)设h(x)=(x+1)2ln(x+1)-x-mx2,
①当$m≤\frac{3}{2}$时,
由(Ⅱ),$h(x)={(x+1)^2}ln(x+1)-x-m{x^2}≥{(x+1)^2}ln(x+1)-x-\frac{3}{2}{x^2}≥0$,
f(x)≥mx2恒成立.
②当$m>\frac{3}{2}$时,h′(x)=2(x+1)ln(x+1)+x-2mx=2(x+1)ln(x+1)-(1-2m)x,
h′′(x)=2ln(x+1)+3-2m,令h′′(x)=0,得${x_0}={e^{\frac{2m-3}{2}}}-1>0$,
当x∈[0,x0)时,h′(x)<h′(0)=0,
∴h(x)在[0,x0)上单调递减∴h(x)<h(0)=0,不成立.
综上,$m≤\frac{3}{2}$.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查不等式的证明和不等式恒成立,注意运用函数的单调性和分类讨论的思想方法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
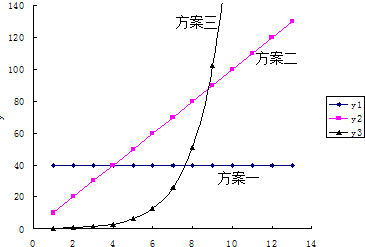
| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | (2,+∞) | D. | $({1,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com