
分析 (1)设出首项和公差,根据等差、等比数列的通项公式和等差数列的前n项和公式,列出方程组求出首项和公差,即可求出an、bn;
(2)假设存在实数p、q、r满足条件,由(1)表示出Tn,利用错位相减法求出Tn的表达式化简后即可求出实数p、q、r的值.
解答 解:(1)设等差数列的公差为d,等比数列的公比为q,
由a1=b1=2,得a4=2+3d,b4=2q3,s4=8+6d,
由a4+b4=27,S4-b4=10得,$\left\{\begin{array}{l}{2+3d+2{q}^{3}=27}\\{8+6d-2{q}^{3}=10}\end{array}\right.$,
解得d=3,q=2,
所以an=3n-1,bn=2n; (6分)
(2)假设存在实数p,q,r,对于任意n∈N*,都有Tn=pan+qbn+r,
由(1)得,Tn=anb1+an-1b2+…+a1bn
=$2{a}_{n}+{2}^{2}{a}_{n-1}+{2}^{3}{a}_{n-2}+…+{2}^{n}{a}_{1}$ ①
∴2Tn=${{2}^{2}a}_{n}+{2}^{3}{a}_{n-1}+{2}^{4}{a}_{n-2}+…+{2}^{n+1}{a}_{1}$ ②
由②-①得,
Tn=-2(3n-1)+3×(22+23+…+2n)+2n+2
=3×$\frac{4(1-{2}^{n-1})}{1-2}$+2n+2-6n+2
=10•2n-6n-10 (12分)
∴Tn=-2(3n-1)+10×2n-12=pan+qbn+r,
可得p=-2;q=10;r=-12,
即存在p=-2;q=10;r=-12满足条件. (14分)
点评 本题考查等差、等比数列的通项公式和等差数列的前n项和公式,错位相减法求出数列的和,考查方程思想,化简、计算能力.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
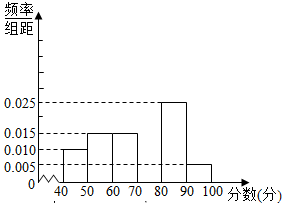 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
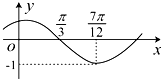
| A. | $\frac{π}{6}$ | B. | $-\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
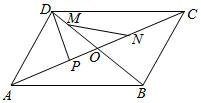 平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com