
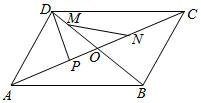
 平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
平行四边形ABCD中,对角线AC与BD相交于点O.已知$\overrightarrow{DP}$⊥$\overrightarrow{AC}$,且|$\overrightarrow{DP}$|=2,$\overrightarrow{DM}$=$\frac{1}{3}$$\overrightarrow{DO}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OC}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.分析 (Ⅰ)根据向量基本定理即可用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{MN}$;
(Ⅱ)根据向量数量积的定义即可求$\overrightarrow{DP}•\overrightarrow{DB}$的值.
解答 解:(Ⅰ)$\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OC}-\frac{2}{3}\overrightarrow{OD}=\frac{1}{3}×\frac{1}{2}\overrightarrow{AC}-\frac{2}{3}×\frac{1}{2}\overrightarrow{BD}=\frac{1}{6}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{BD}$=$\frac{1}{6}(\overrightarrow{AB}+\overrightarrow{AD})-\frac{1}{3}(\overrightarrow{AD}-\overrightarrow{AB})=\frac{1}{2}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AD}$=$\frac{1}{2}a-\frac{1}{6}b$.-----------------------(6分)
(Ⅱ)$\overrightarrow{DP}•\overrightarrow{DB}=\overrightarrow{DP}•2\overrightarrow{DO}=\overrightarrow{DP}•2(\overrightarrow{DP}+\overrightarrow{PO)}=2{|{\overrightarrow{DP}}|^2}+\overrightarrow{DP}•\overrightarrow{PO}$--------------------(9分)
∵$\overrightarrow{DP}⊥\overrightarrow{AC}$,∴$\overrightarrow{DP}•\overrightarrow{PO}=0$,又$|{\overrightarrow{DP}}|=2$,
∴$\overrightarrow{DP}•\overrightarrow{DB}=2|\overrightarrow{DP}{|^2}=2×{2^2}=8$.-----------------------(12分)
点评 本题主要考查向量基本定理的应用以及向量数量积的计算,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,记甲、乙两人得分的标准差分别为s1、s2,则下列判断正确的是( )
甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,记甲、乙两人得分的标准差分别为s1、s2,则下列判断正确的是( )| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s1<s2 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s1>s2 | C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s1<s2 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{1}{m}$)>-$\frac{1}{m}$ | B. | f($\frac{1}{m}$)>-$\frac{1}{m+1}$ | C. | f($\frac{1}{m+1}$)<$\frac{m}{m+1}$ | D. | f($\frac{1}{m+1}$)<-$\frac{m+2}{m+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com